BUT2FI_R4.B.10/td_tp/tp3

TP3

Le but du tp est de mettre en oeuvre une communication sécurisée entre un client et un serveur, en deux phases :

• Echange d'une clé.
• Cryptage de la communication par un algorithme de chiffrement symétrique à l'aide de la clé echangée. (XTEA pour ce tp)

Rappel de cours

Diffie-Hellman

Le système (et sa sécurité) de Diffie-Hellman repose sur la difficulté pratique, pour des grands nombres, de calculer le logarithme discret dans un groupe multiplicatif \mathbb{Z}_{p}^{*} avec p premier.

On rappelle que lorsque p est premier, \mathbb{Z}_{p}^{*} est cyclique. Si g est un générateur, tout élément x\in \mathbb{Z}_{p}^{*} s'écrit (de manière unique) sous la forme

x=g^a,\ \ 1\leq a \leq p-1

Par définition, a est le logarithme (discret) de x dans la base g noté

a=\log_{g}(x)

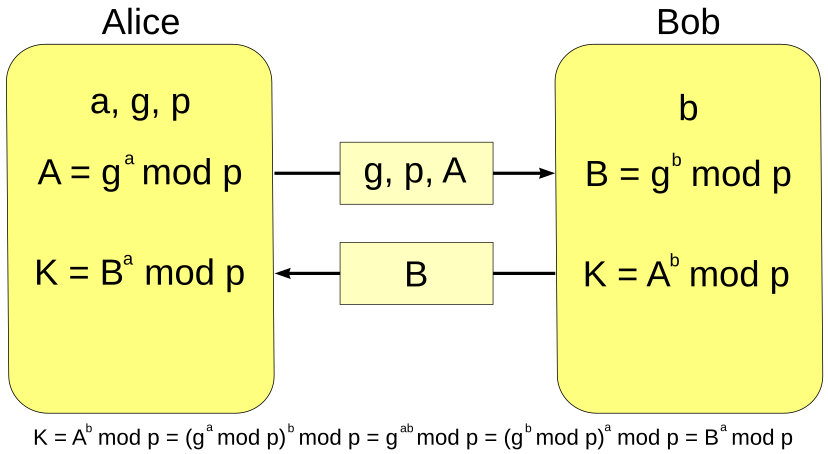
Le schéma en haut de la page illustre comment deux entités peuvent échangés une clef. Alice génére p, un générateur g. Il choisit un nombre aléatoire a (2\leq a\leq p-2), et envoie à Bob le triplet ((p,g,g^a). Bob recoit le triplet, et choisit un nombre b. Il envoie à Alice g^b. La clé calculée par Alice, et Bob est

| (g^a)^b = (g^b)^a= g^{ab} ]

Pour calculer la clé, il faut connaître ab. Or seuls g^a et g^b ont été échangés. Ce qui nous ramène au problème du logarithme discret qui est difficile en pratique pour des grands nombres.

Votre travail

Le but du tp est d'écrire un client/serveur TCP :

• Le client et le serveur utilise Diffie-Hellman pour échanger une clé sur 16 octets. On utilisera des nombres premiers de Sophie Germain.
• Le client saisit un message de l'utilisateur, le chiffre avec XTEA, et envoit le message chiffré.
• Le serveur reçoit le message chiffré, le déchiffre, et l'affiche.

1. Trouver un générateur peut-être long. En effet, tout ce qu'on l'on sait sur l'ordre d'un élément de \mathbb{Z}_p^{*}, c'est qu'il divise l'ordre du groupe, i.e p-1. Pour que la vérification soit plus rapide, on s'interesse aux nombres premiers dit de Sophie Germain. Ils ont la particularité d'être sous la forme 2q+1, avec q premier. Ainsi, l'ordre de \mathbb{Z}_{p}^{*} est 2q. L'ordre possible d'un élément ne peut être que 2, q ou 2q. Ce qui fait peu (combien) de test à effectuer quand on cherche un générateur.

   Ecrire un script à l'aide de la commande primesieve qui donne tous les nombres premiers de Sophie Germain dans [2^{62},2^{62}+20000]. (il faut quelques minutes. Assurez-vous que votre shell permet de représenter de tels nombres. Comment ?)

2. Ecrire les fonctions suivantes :

   typedef unsigned __int128 uint128;
   typedef unsigned long long int uint64;
   
   uint64 expm(uint64 m, uint64 e, uint64 n);
   // calcule m^e modulo n
   uint64 generateur(uint64 p);
   // calcule un generateur de (Zp)*
   // en supposant que p est un nombre premier 
   // de Sophie Germain
   

   Testez (test_df.c) avec p = 4611686018427402023 pour trouver un générateur.

Remarque : pour la génération d'un grand nombre premier, utilisez le programme primesieve qsui se trouve dans

/export/documents/info/is1+2/asr

.