# TP javascript : bases du langages.
Un peu [d'aide](./aide.md).
> - seance 1 : [révisions](#p1)
> - seance 2 : [forEach, filter, map, reduce, etc.](#p2)

### <a name="p1"></a> Séance 1
#### Ex1 : fourmi de Langton
Une fourmi, assimilable à un petit automate, se promène sur une grille de points colorés; 
pour commencer, tous les points sont blancs.
- la fourmi est initialement placée au centre de la grille. Elle se déplace dans les quatre directions cardinales. Initialement, elle va vers l'est.
- A chaque pas, elle se déplace d'une case dans sa direction. Son parcours est dicté par les deux règles suivantes :
  - Si la case atteinte est noire, elle la repeint en blanc, et tourne de 90° à gauche.
  - Si la case est blanche, elle la repeint en noire, et tourne de 90° à droite.
- Elle continue son chemin en suivant ces règles.


<div align="center">
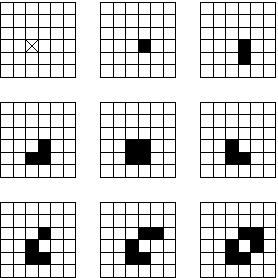
_Les 9 premiers pas de la fourmi_<br>
<img src="./img/fourmi.png">
</div>

Vous disposez de [sources](./src/langton)  que vous allez compléter. En particulier, il y a 2 modules :

>- une classe **Ant** qui représente l'univers : la fourmi, et les tuiles sur lesquelles elle se déplace.
>- une fonction **render** qui gére l'affichage graphique.


- La fourmi a une position sur la grille, ainsi qu'une direction. La direction sera codée par un entier (angle 0,90,180 ou 270).
- Les tuiles sont repréntées par un tableau à 2 dimensions. Chaque tuile a 2 valeurs possibles (0 ou 1).


1. Complétez le code de la classe `Ant`.
2. Complétez le code de `app.js`.
3. Ajoutez un bouton/lien qui permet de réinitialiser la simulation.
4. Dissociez, en terme de classe/structure, la fourmi de la grille sur laquelle elle évolue, et modifiez le
   code en conséquence.

<div align="center">
<img src="./img/langton.png">
</div>


#### Ex2 : fourmi de Langton
On peut complexifier et généraliser la fourmi précédente, et les règles d'évolution de l'automate correspondant : la fourmi, et les tuiles peuvent avoir 
un nombre quelconque d'états. Les règles de l'automate sont alors décrites par une table de transition.

Exemple 1 : on donne la table de transition suivante (T désigne la tuile, a la fourmi) à 2 états pour la fourmi, et 2 états pour les tuiles.


|      | T: 0      | T: 1      |
|------|-----------|-----------|
| a: 0 | (1,0,1)   | (0,90,1) |
| a: 1 | (0,-90,1)  | (1,0,1)   |



Chaque triplet représente  (Ant State Change, Ant Direction Change, Tile State Change). Ainsi,

- (1,90,0)  => on incrémente 1 à l'état de la fourmi, 90 à sa direction, et 0 à l'état de la tuile.
- (0,-90,1) => on incrémente 0 à l'état de la fourmi, -90  à sa direction, et 1 à l'état de la tuile.

Les incrémentations se font modulo le nombre d'états possibles.

Avec cet automate, on obtient la figure :

<div align="center">
<img src="./img/langton1.png">
</div>

Par commodité, on note la table de transition précédente simplement :

```
 (1,0,1)    (0,90,1) 
 (0,-90,1)   (1,0,1)   
```

1. Modifiez le code de l'exercice 1 de manière à pouvoir simuler l'automate ci-dessus. Votre solution doit pouvoir permettre une simulation quelconque.
   Quelle est la table correspondante à la fourmi de la première partie du tp ?
2. Testez avec 
   ```
   (1,90,0) (0,-90,1)
   (0,-90,1) (1,90,1)
   ```
	<div align="center">
	<img src="./img/langton2.png">
	</div>
3. Testez avec 

   ```
   (1, 0, 1) (0, 90, 0) 
   (0, -90, 1) (1, 0, 1)
   ```

### <a name="p2"></a> Séance 2
#### Ex1 

Soit le tableau d'objets suivant :
```js
let customers = [
	{
		'id': 1,
		'f_name': 'Abby',
		'l_name': 'Thomas',
		'gender': 'M',
		'married': true,
		'age': 32,
		'expense': 500,
		'purchased': ['Shampoo', 'Toys', 'Book']
	},
	{
		'id': 2,
		'f_name': 'Jerry',
		'l_name': 'Tom',
		'gender': 'M',
		'married': true,
		'age': 64,
		'expense': 100,
		'purchased': ['Stick', 'Blade']
	},
	{
		'id': 3,
		'f_name': 'Dianna',
		'l_name': 'Cherry',
		'gender': 'F',
		'married': true,
		'age': 22,
		'expense': 1500,
		'purchased': ['Lipstik', 'Nail Polish', 'Bag', 'Book']
	},
	{
		'id': 4,
		'f_name': 'Dev',
		'l_name': 'Currian',
		'gender': 'M',
		'married': true,
		'age': 82,
		'expense': 90,
		'purchased': ['Book']
	},
	{
		'id': 5,
		'f_name': 'Maria',
		'l_name': 'Gomes',
		'gender': 'F',
		'married': false,
		'age': 7,
		'expense': 300,
		'purchased': ['Toys']
	},
	{
		'id': 6,
		'f_name': 'Homer',
		'l_name': 'Simpson',
		'gender': 'M',
		'married': true,
		'age': 39,
		'expense': 500,
		'purchased': ['Book']
	}
];
```

En utilisant les fonctions/méthodes `forEach, filter, map, reduce, some, every, find`, donnez ou calculez :
1. un tableau des client séniors (dont l'âge est plus de 60 ans).
2. un tableau où chaque client possède un nouvel attribut `full_name`.
3. s'il y a un client de moins de 10 ans.
4. le nombre d'acheteurs de livres.
5. la somme totale d'argent dépensé par les clients marriés.
6. Pour chaque produit, la liste (`id`) des acheteurs. 

#### Ex2 
Ecrire une fonction qui calcule tous les nombres premiers inférieurs à une valeur entière `n` donnée,
en utilisant le [crible d'Erastosthène](https://fr.wikipedia.org/wiki/Crible_d%27%C3%89ratosth%C3%A8ne).

Le version du crible est volontairement "mal écrite" en terme de performance :

```js
let eratosthene1 = n => {
	let numbers = Array.from({length : n - 2}, (v,k) => k + 2);
	let p ,primes = [];

	while(numbers.length){
		[p,...numbers] = numbers;
		numbers = numbers.filter( k => k%p != 0);
		primes = [...primes,p];
	}
	return primes;
}
```

1. Expliquez précisément ce code. Testez et dites pourquoi qu'il n'est pas efficace. 
2. Écrivez une version plus efficace et comparer les temps de calcul. Vous pourrez compléter le code suivant :

```js
let  eratosthene = n => {

 let primes = []; 
 let filterArray = []; // tableau qui permet
					   // de cribler les multiples des nombres
                       // premiers

 for(let i = 2; i <= n; i++){
	 // TODO
 }
 return primes;
}
```