SAE_2.04/EXO2

Exercice 2 : Analyse des âges et de l'expérience

Table des matières

1. Initialisation des variables
2. Distribution des âges
3. Distribution de l'expérience
4. Statistiques descriptives pour l'âge
5. Boîte à moustaches pour l'âge
6. Statistiques descriptives et boîte à moustaches pour l'expérience

---

Initialisation des variables

Pour cette exercice, veuillez initaliser les variables suivantes :

Script Scilab :

D = csvRead('data.csv');
DD = csvRead('data.csv',',','.','string');
genre = DD(:,3);

---

Question 1 : Distribution des âges

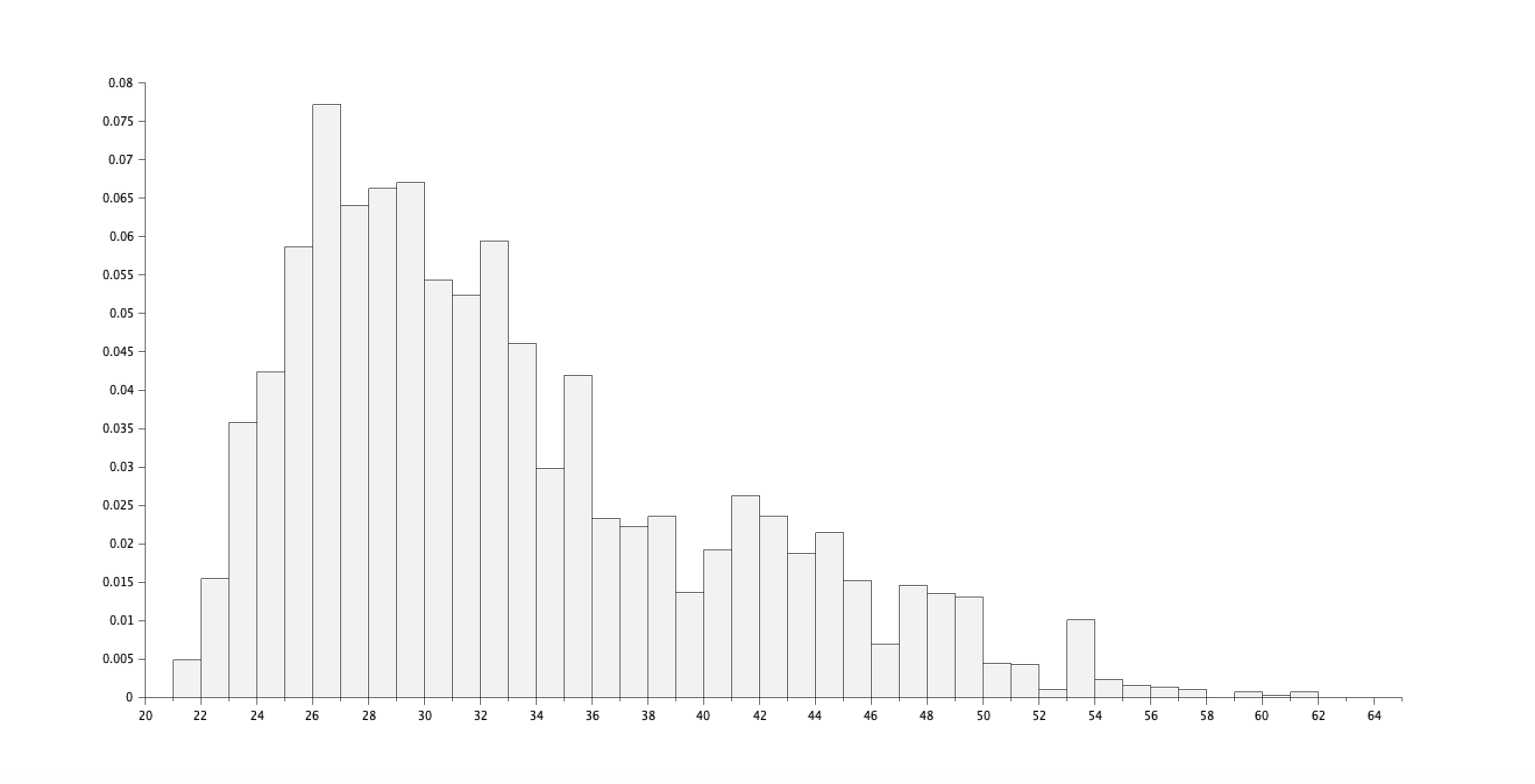
Donnez sous forme d'histogramme la distribution des âges.

Script Scilab :

age = D(:, 2);
min_age = min(age); 
max_age = max(age);  
histplot(41,age);

Résultat :

---

Question 2 : Distribution de l'expérience

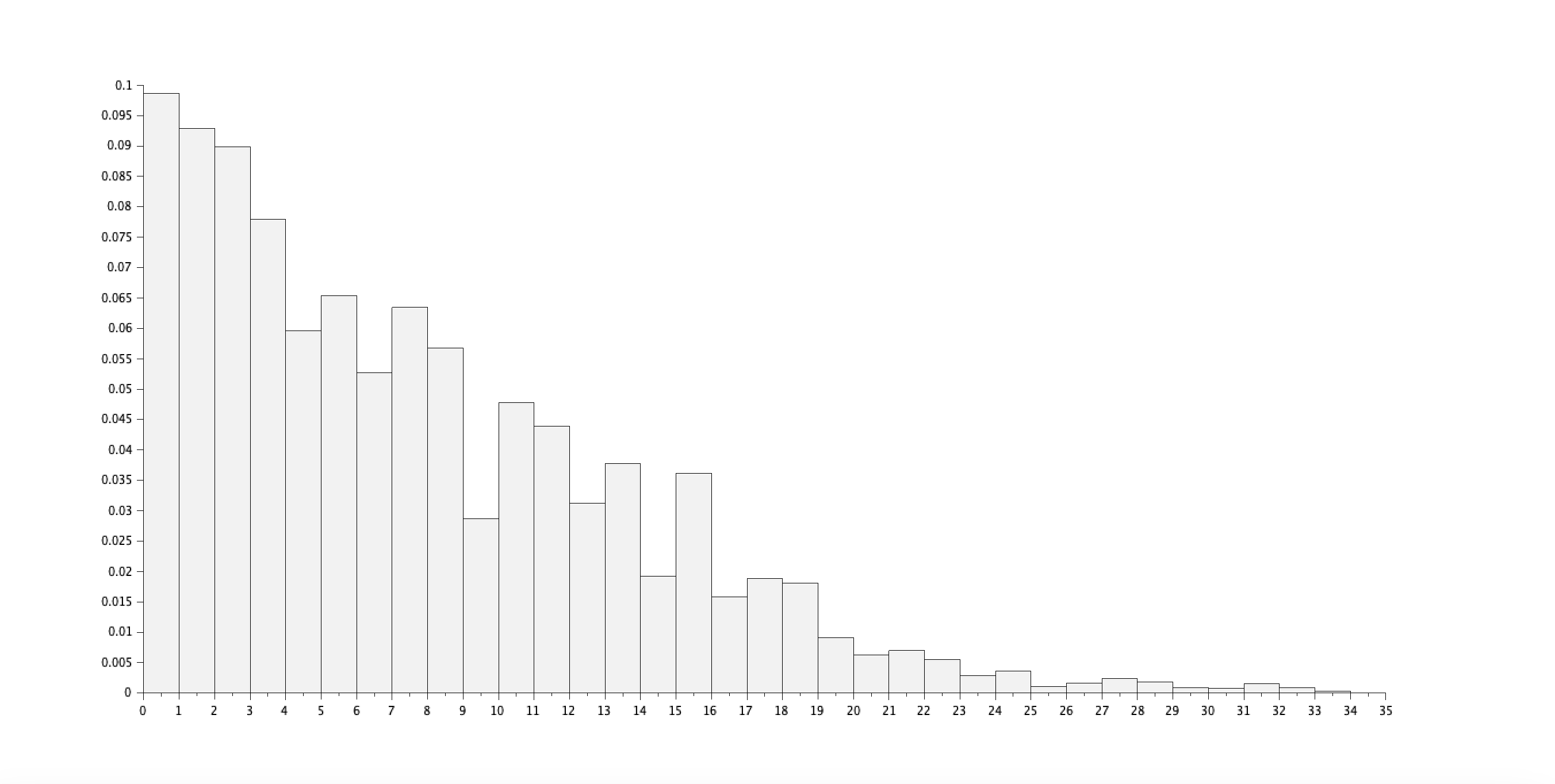
Donnez sous forme d'histogramme la distribution de l'expérience.

Script Scilab :

exp = D(:,6);
min_xp = min(exp);
max_xp = max(exp);
histplot(34,exp);

Résultat :

---

Question 3 : Statistiques descriptives pour l'âge

Donnez les quartiles, interquartiles, min, max, moyenne, médiane, mode, et écart type de l'âge.

Script Scilab :

Q = quart(age)
IQR = Q(3) - Q(1) 
min_age = min(age);
max_age = max(age);
mean(age)
median(age)

unique_vals = unique(age);
freq = histc(ages, unique_vals);
[max_freq, max_index] = max(freq);
age_mode = unique_vals(max_index);

stdev(age)

Résultat :

• Quartiles : [28, 32, 38]
• Interquartile Range (IQR) : Q(3) - Q(1) = 10
• Minimum : 21
• Maximum : 62
• Moyenne : 33.622033
• Médiane : 32
• Mode : 26
• Écart type de l'âge : 7.6156456

---

Question 4 : Boîte à moustaches pour l'âge

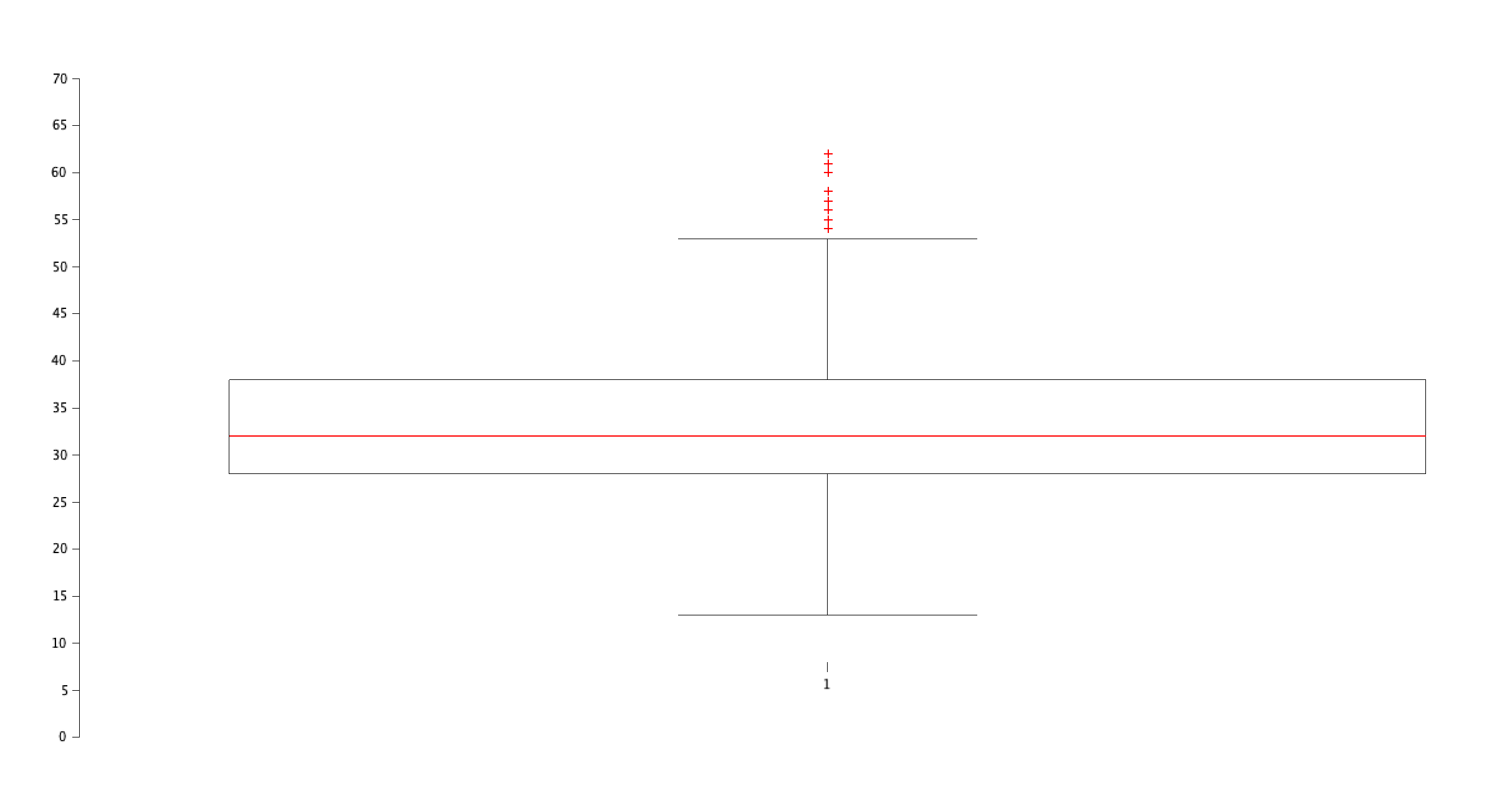
A l'aide du paquet stixbox, tracez une boîte à moustaches pour l'âge.

Script Scilab :

boxplot(age);

Résultat :

---

Question 5 : Statistiques descriptives et boîte à moustaches pour l'expérience

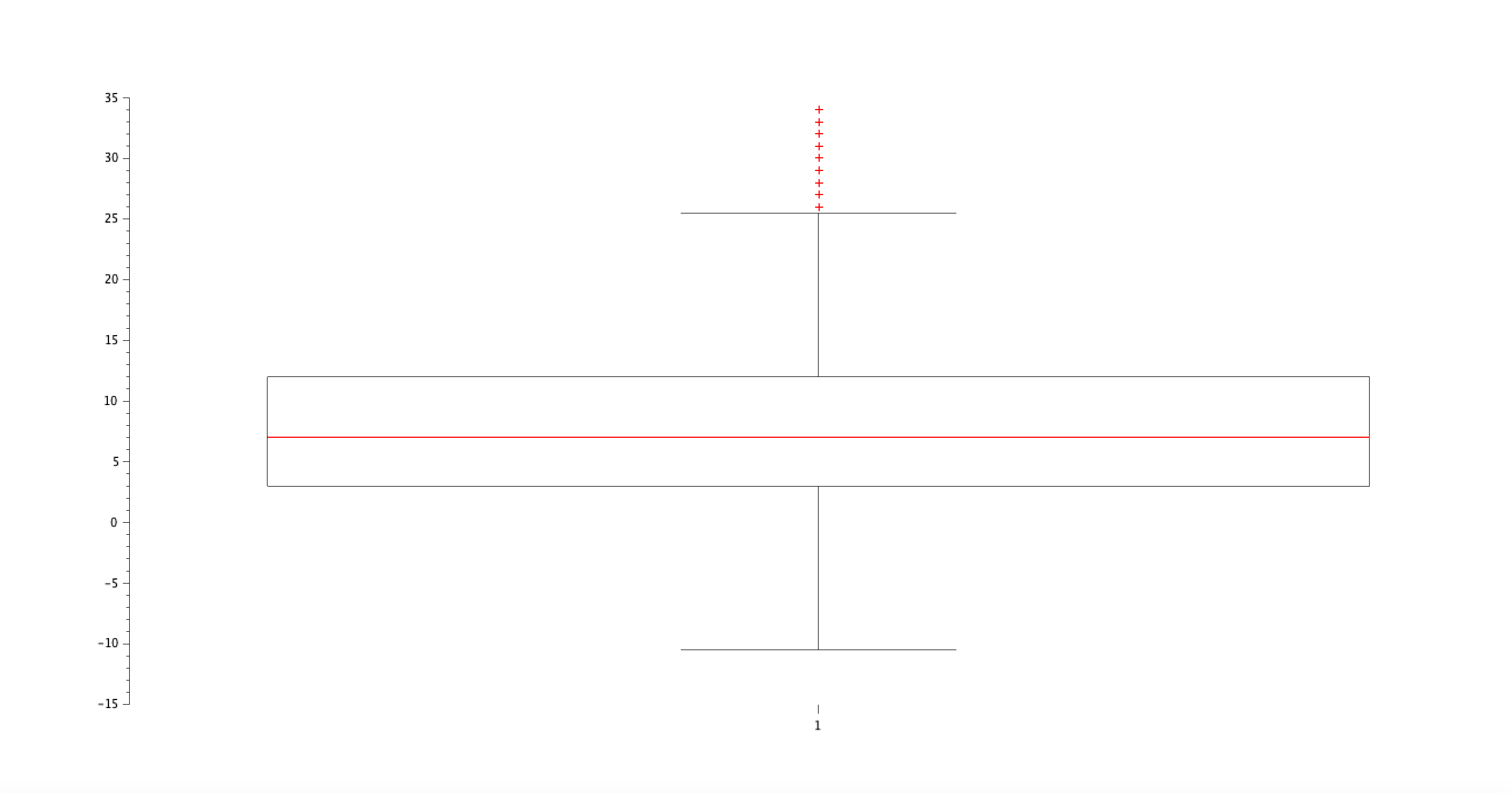
Refaire les questions précédentes pour l'expérience.

Script Scilab :

Q = quart(exp) 
IQR = Q(3) - Q(1)
min_xp = min(exp); 
max_xp = max(exp); 
mean(exp)
median(exp)

Unique_vals = unique(exp);
Freq = histc(exp, Unique_vals);
[max_Freq, max_Index] = max(Freq);
exp_mode = Unique_vals(max_Index);

stdev(exp)


boxplot(exp);

Résultat :

• Quartiles : [3, 7, 12]

• Interquartile : Q(3) - Q(1) = 9

• Minimum : 0

• Maximum : 34

• Moyenne : 8.0950142

• Médiane : 7

• Mode : 1.5

• Écart type : 6.0598534

---

⬅️ | 🏠 | ➡️