SAE_2.04/EXO3

Exercice 3 : Analyse des salaires

Table des matières

1. Initialisation des variables
2. Distribution des salaires par genre
3. Histogramme des salaires moyens par niveau d'études
4. Statistiques descriptives des salaires
5. Répartition des salaires par genre

---

Initialisation des variables

Pour cette exercice, veuillez initaliser les variables suivantes :

Script Scilab :

csvDouble = csvRead("data.csv")                         //ouvre data.csv en une matrice d'entier
csvString = csvRead("data.csv",[],[],'string')          //ouvre data.csv en une matrice de string

---

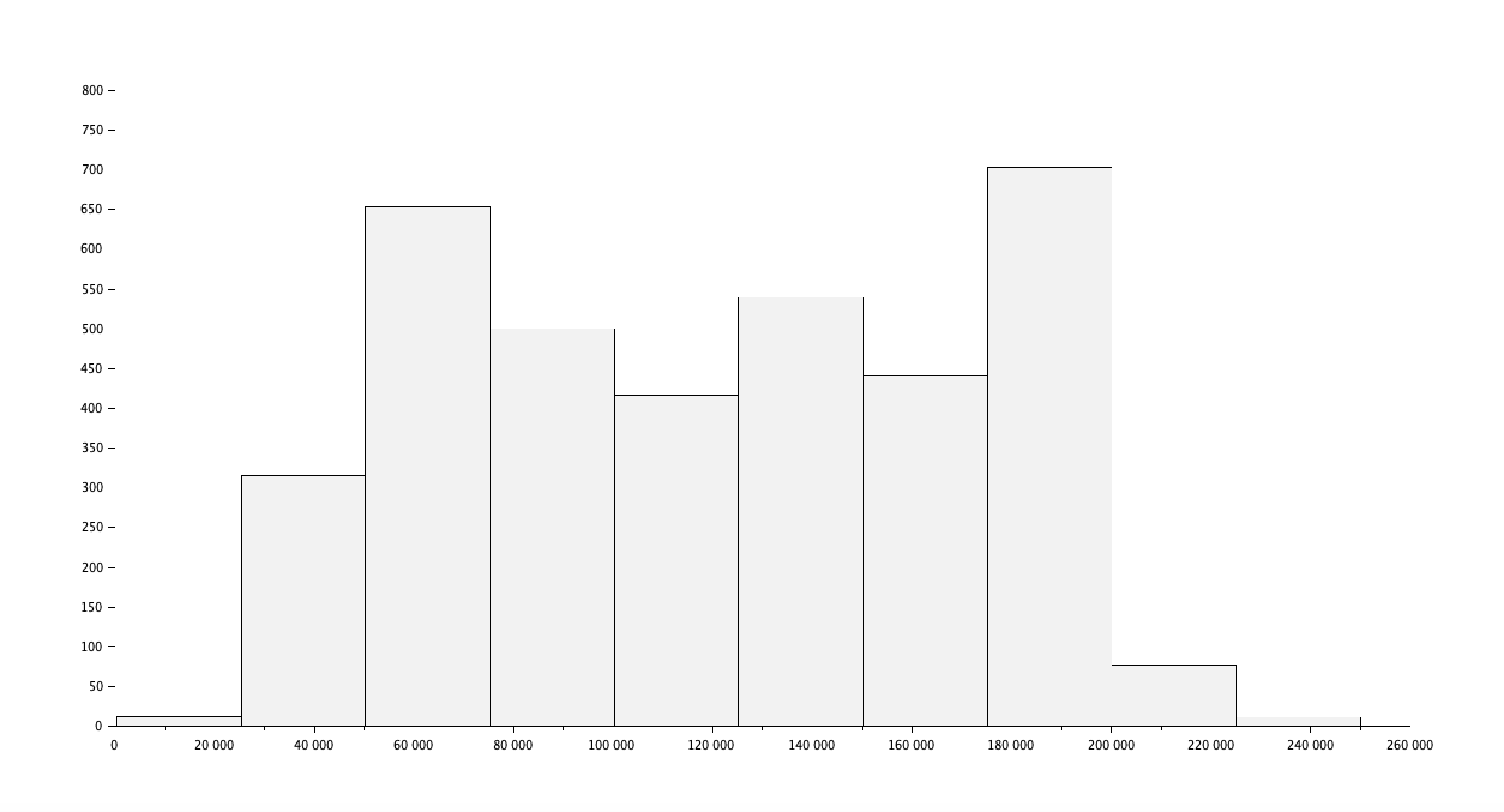
Question 1 : Distribution des salaires par genre

Donnez, sous forme d'histogramme, la distribution des salaires suivant le genre.

Script Scilab - hommes :

id_male = find(csvString(:,3) == "Male" )
salaire_male = csvDouble(id_male,7)
histplot(10,salaire_male,normalization=%f)

Script Scilab - femmes :

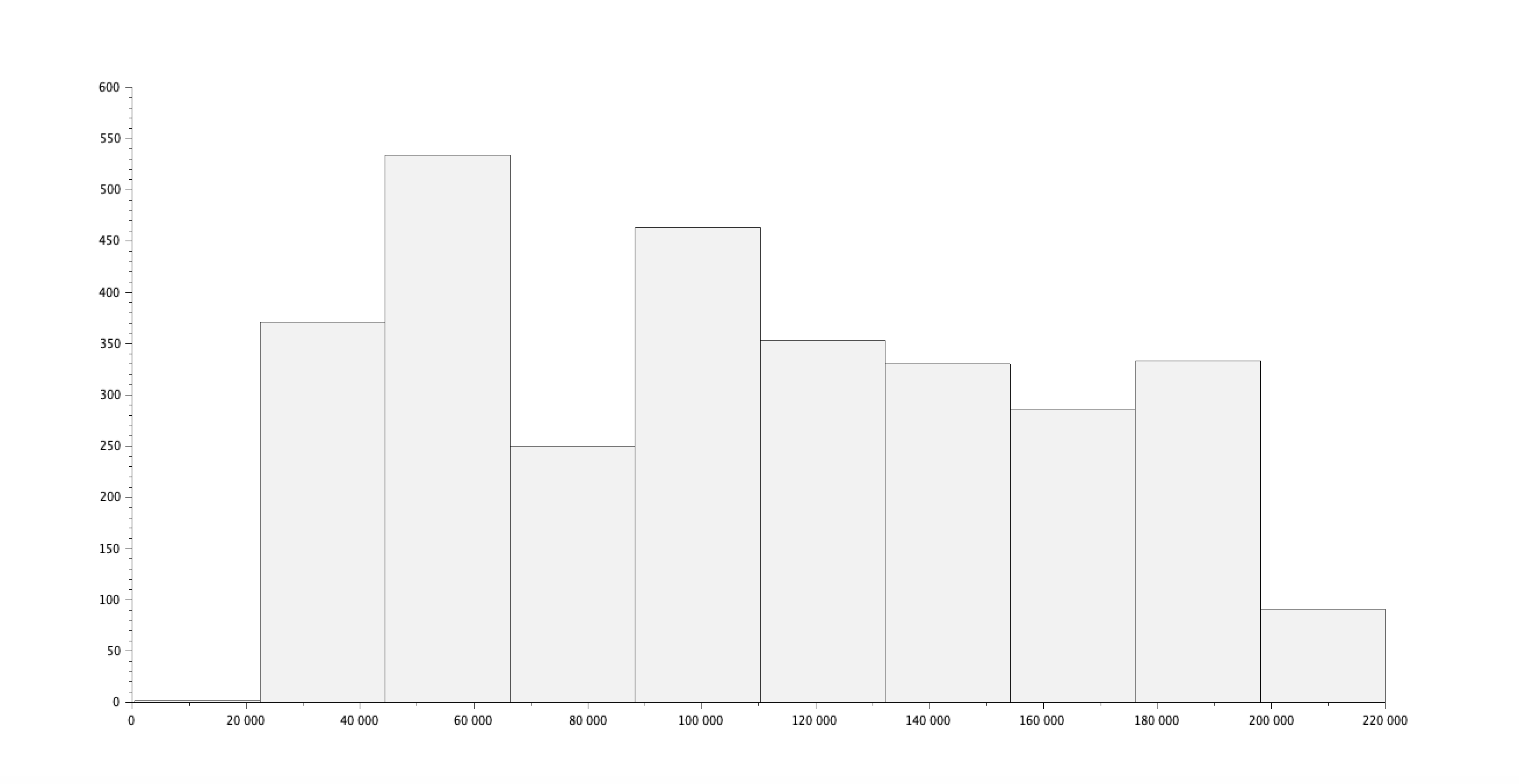
id_female = find(csvString(:,3) == "Female" )
salaire_female = csvDouble(id_female,7)
histplot(10,salaire_female,normalization=%f)

Script Scilab - autres :

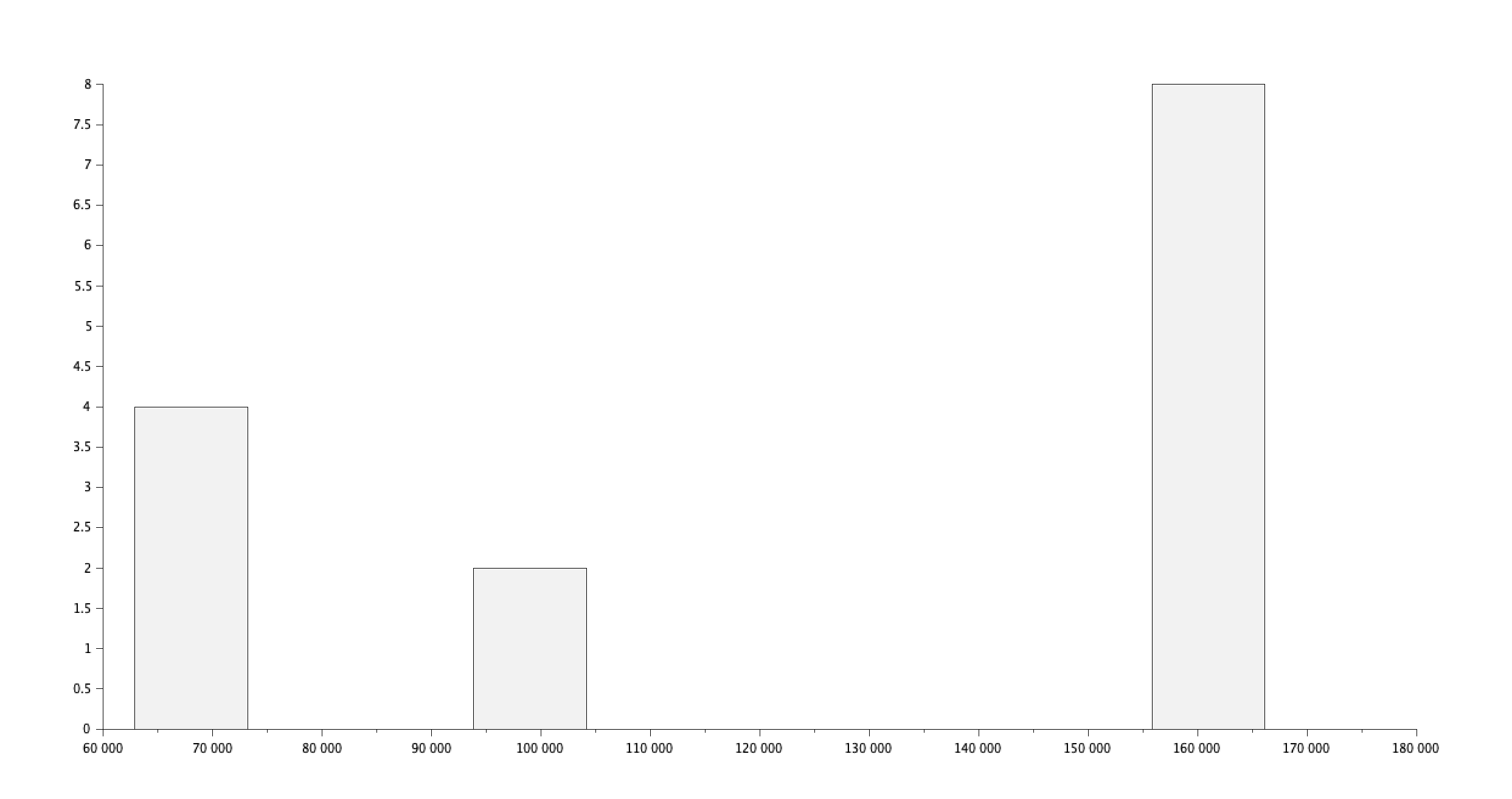
id_other = find(csvString(:,3) == "Other" )
salaire_other = csvDouble(id_other,7)
histplot(10,salaire_other,normalization=%f)

Résultat :

Hommes :

Femmes :

Autres :

---

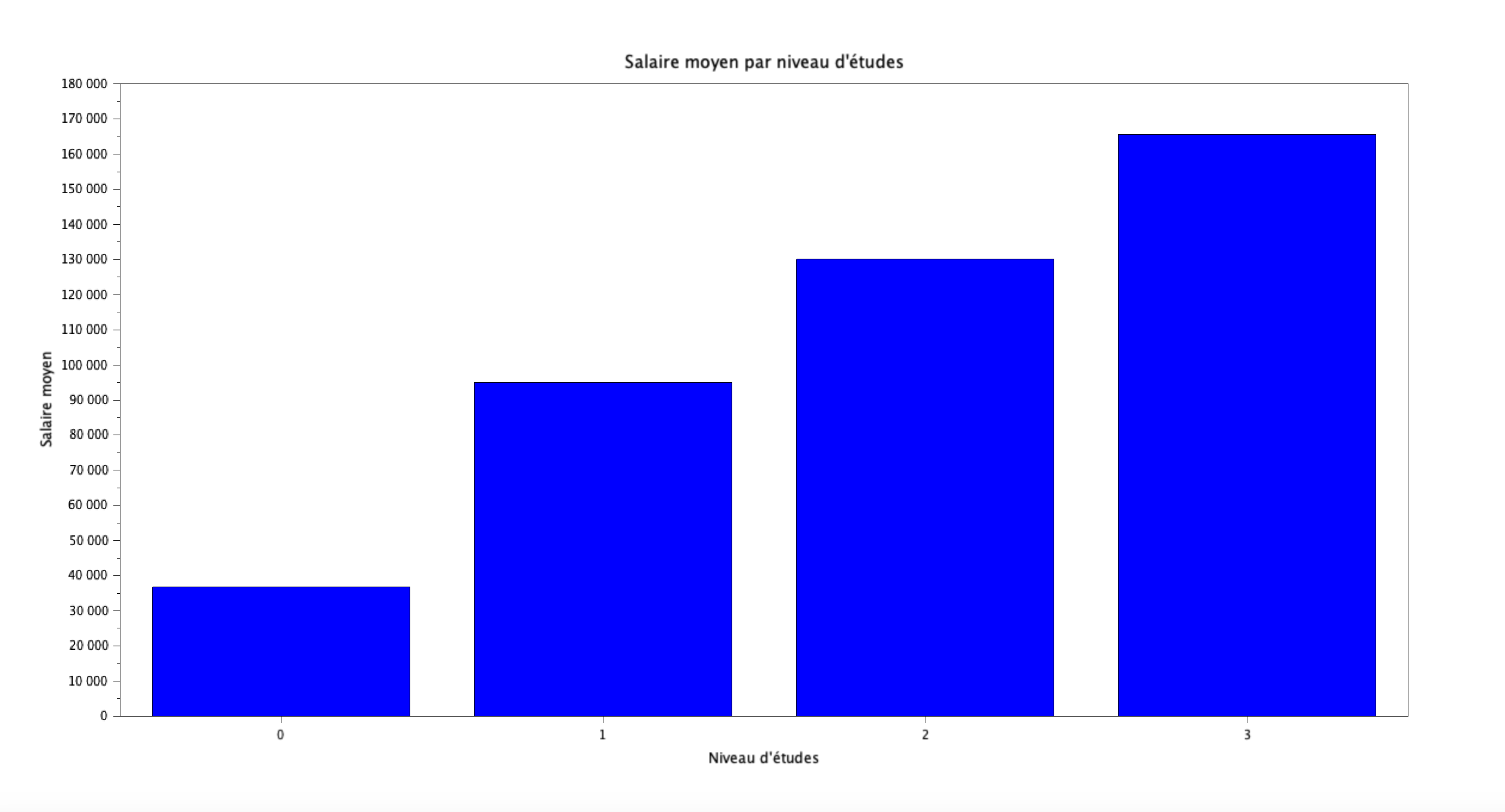
Question 2 : Histogramme des salaires moyens par niveau d'études

Tracez un histogramme des salaires moyens suivant le niveau d'études.

Script Scilab :

indice_high = find(csvDouble(:,4) == 0 )
salaire_high = csvDouble(indice_high,7)
moy_h = mean(salaire_high)                                      


indice_b = find(csvDouble(:,4) == 1 )
salaire_b = csvDouble(indice_b,7)
moy_b = mean(salaire_b)                                         


indice_m = find(csvDouble(:,4) == 2 )
salaire_m = csvDouble(indice_m,7)
moy_m = mean(salaire_m)                                         


indice_p = find(csvDouble(:,4) == 3)
salaire_p = csvDouble(indice_p,7)
moy_p = mean(salaire_p)                                         


matrice = [moy_h,moy_b,moy_m,moy_p]
bar([0,1,2,3],matrice)

xlabel("Niveau d''études");
ylabel("Salaire moyen");
title("Salaire moyen par niveau d''études");

Résultat :

---

Question 3 : Statistiques descriptives des salaires

Donnez les quartiles, interquartiles, minimum, maximum, moyenne, médiane, et écart-type des salaires. Tracez une boîte à moustaches.

Script Scilab :

mean(csvDouble(:,7))        //moyenne
min(csvDouble(:,7))         //min
max(csvDouble(:,7))         //max
median(csvDouble(:,7))      //médianne
quart(csvDouble(:,7))       //quartile
iqr(csvDouble(:,7))         //interquartile
stdev(csvDouble(:,7))       //ecart-type

sal = tabul(csvDouble(:,7));
[occurence_tri,indice_tri] = gsort(sal(:,2));
liste_exp = sal(:,1);
mode = liste_exp(200)        //mode

atomsLoad("stixbox")
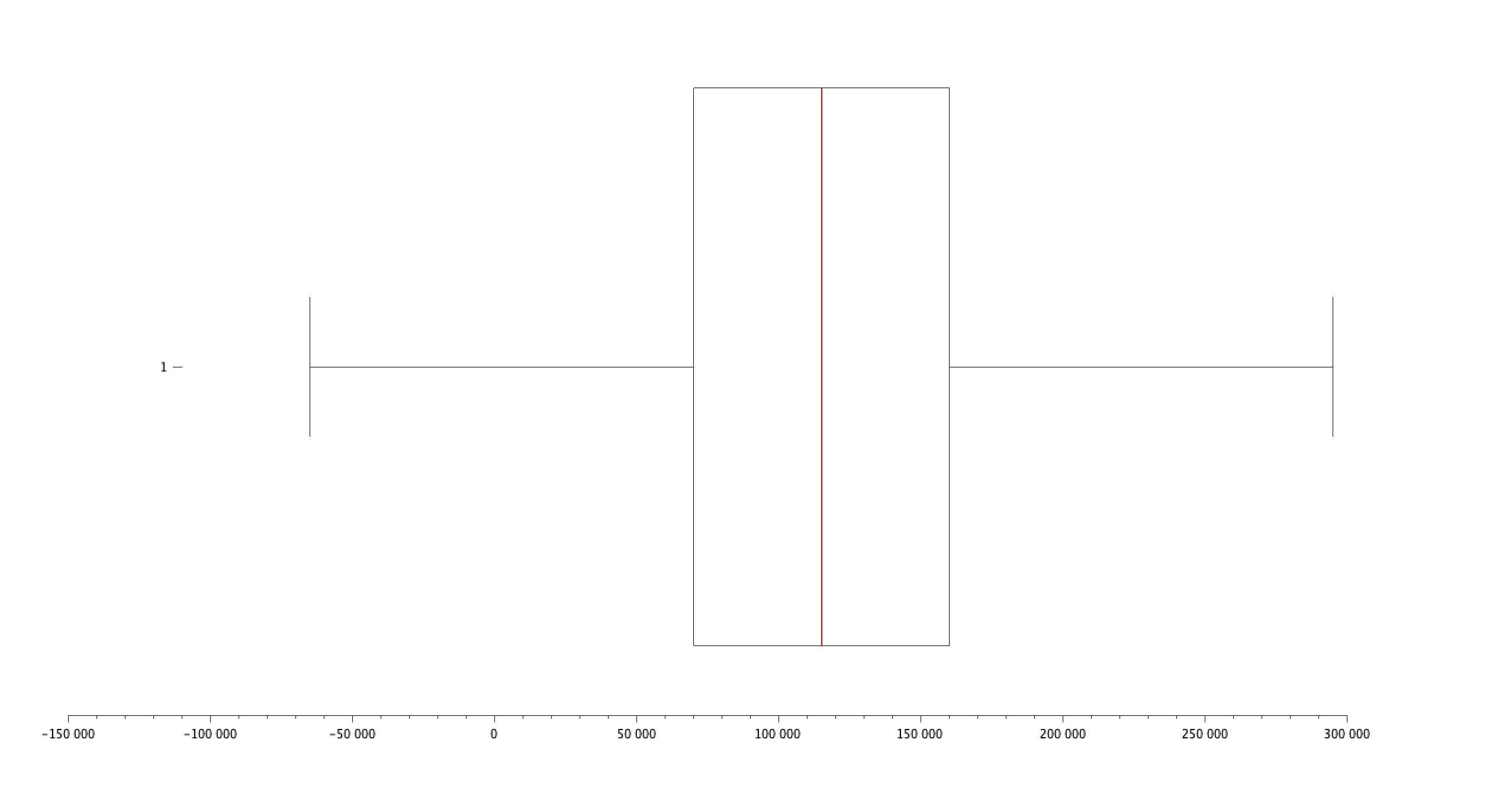
boxplot(csvDouble(:,7),"orientation","horizontal")

Résultat :

• Quartiles : [Q1, Q2 (médiane), Q3] = [70000, 115000, 160000]
• Interquartile Range (IQR) : Q(3) - Q(1) = 90000
• Minimum : 350
• Maximum : 250000
• Moyenne : 115326.96
• Médiane : 115000
• Mode : 140000
• Écart-type : 52786.184

---

Question 4 : Répartition des salaires par genre

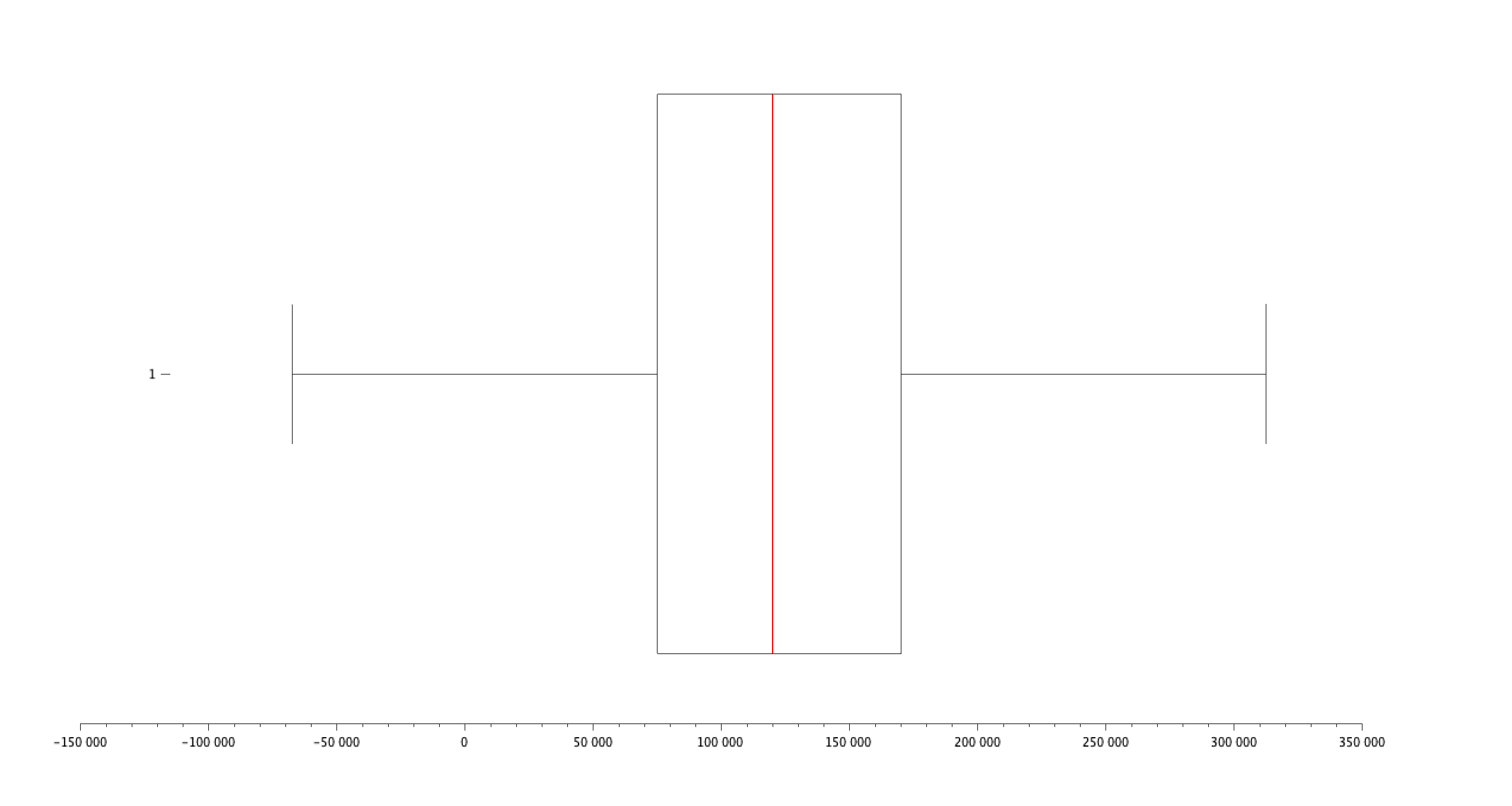
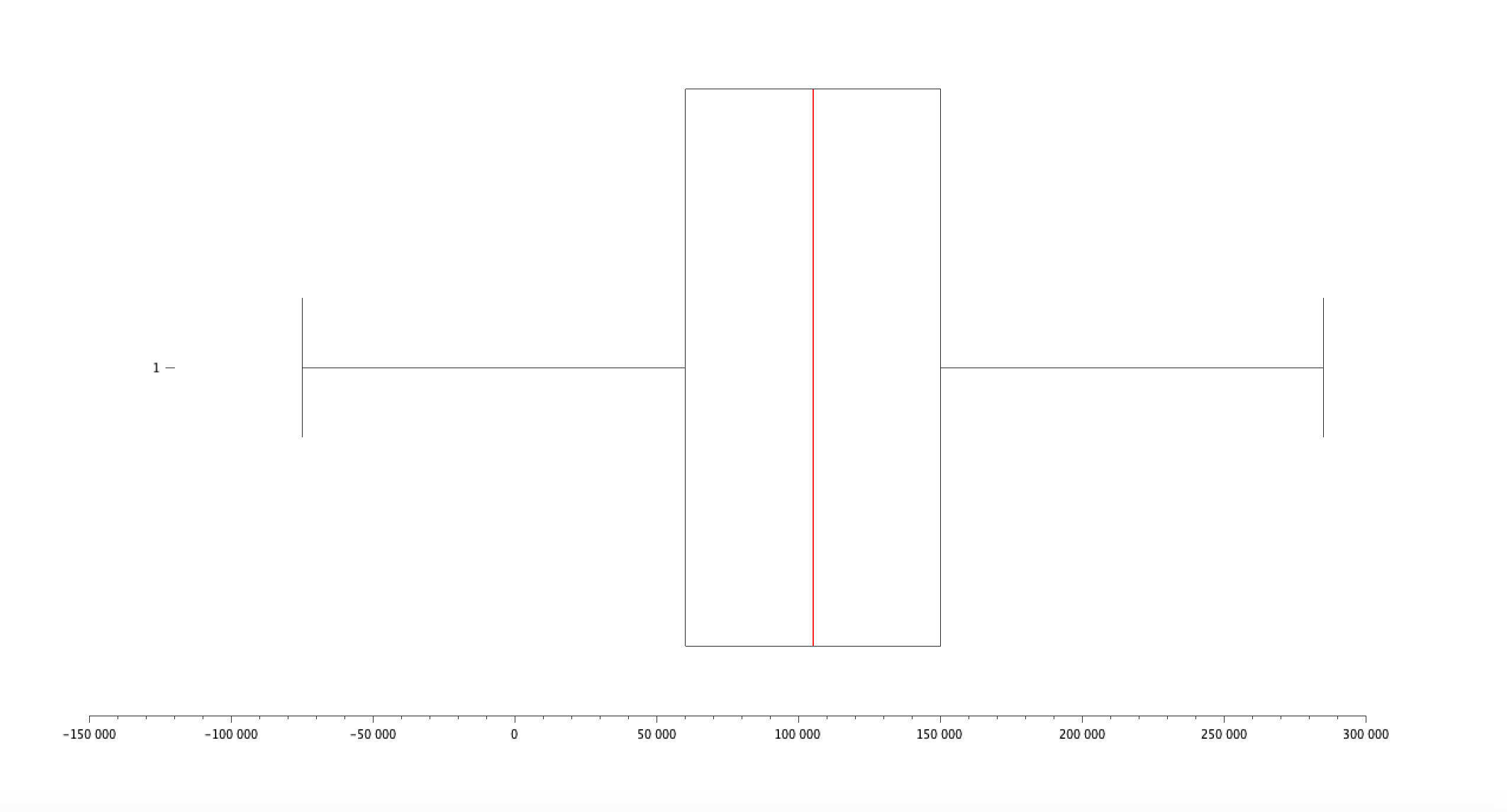
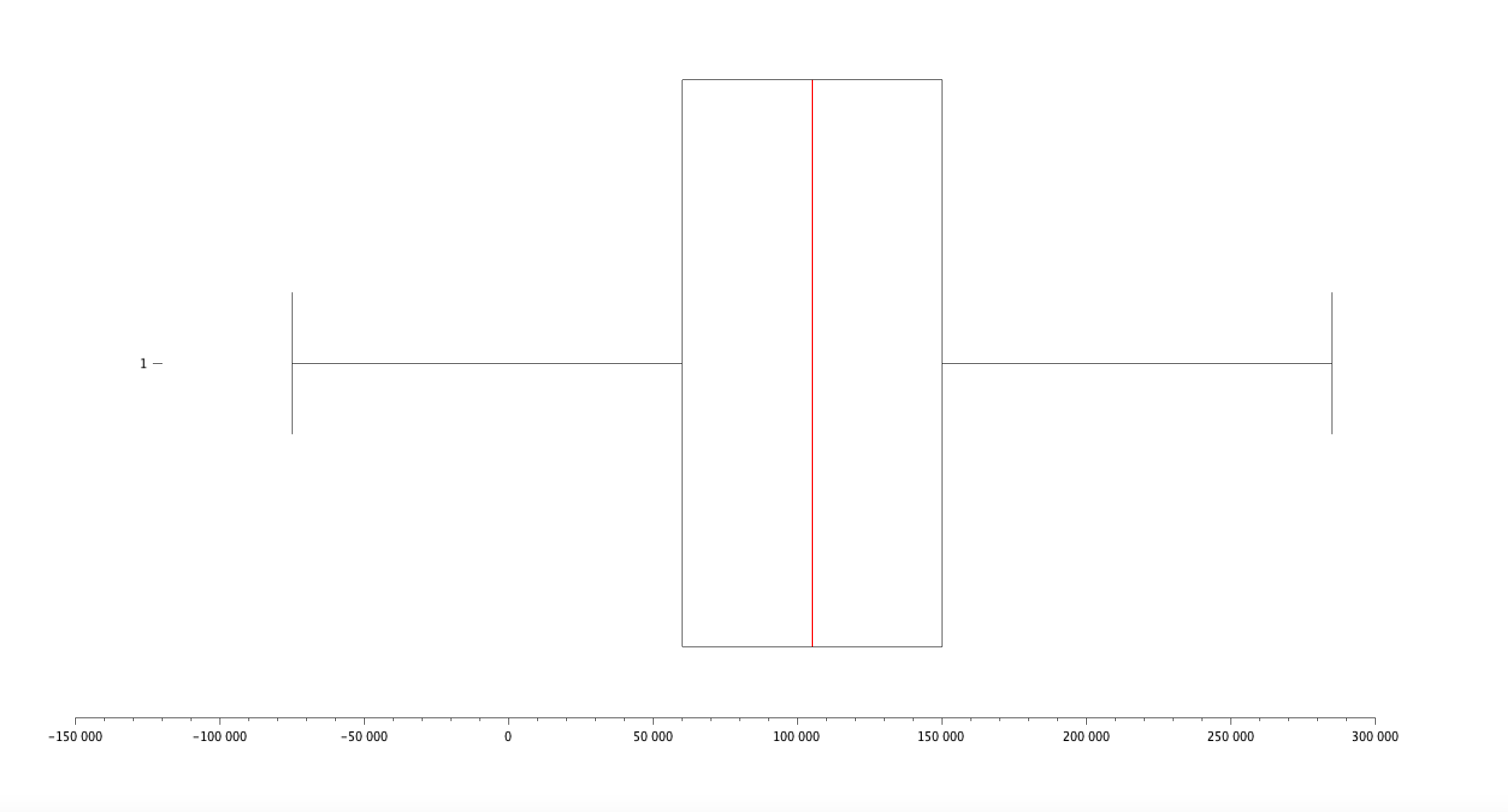
Refaire la question précédente, en distinguant les genres. Tracez une boîte à moustache pour chaque genre. Commentaires ?

Script Scilab :

MARCO ???
MARCO ???
MARCO ???
MARCO ???
MARCO ???
MARCO ???


MARCO ???
MARCO ???MARCO ???MARCO ???
MARCO ???
MARCO ???
MARCO ???

Résultat :

• Hommes :

  • Quartiles : [Q1, Q2 (médiane), Q3] = [..., ..., ...]
  • Interquartile Range (IQR) : QH(3) - QH(1) = ...
  • Minimum : ...
  • Maximum : ...
  • Moyenne : ...
  • Médiane : ...
  • Écart-type : ...

  

• Femmes :

  • Quartiles : [Q1, Q2 (médiane), Q3] = [..., ..., ...]
  • Interquartile Range (IQR) : QF(3) - QF(1) = ...
  • Minimum : ...
  • Maximum : ...
  • Moyenne : ...
  • Médiane : ...
  • Écart-type : ...

  

• Femmes :

  • Quartiles : [Q1, Q2 (médiane), Q3] = [..., ..., ...]
  • Interquartile Range (IQR) : QF(3) - QF(1) = ...
  • Minimum : ...
  • Maximum : ...
  • Moyenne : ...
  • Médiane : ...
  • Écart-type : ...

  

• Commentaires : ...

---

⬅️ | 🏠 | ➡️