TD4 - DEV5.1 Qualité algorithmique

Complexité algorithmique

Ex 2 - Calculs de complexité de fonctions

Calculez la complexité des fonctions suivantes :

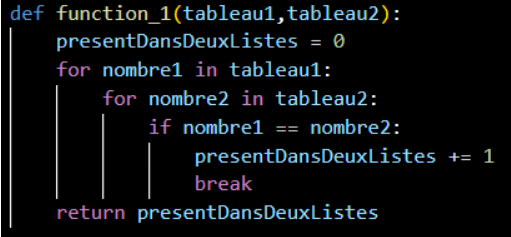
Ici on prend un tableau 1 contenant n valeurs et un tableau 2 contenant m valeurs.

On parcour entièrement les deux pour savoir si une valeur ce trouve dans l'autre tableau.

On a donc :

O ( n x m )

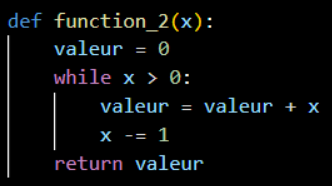
Ici on prend un une variable x de valeur n.

Tant que x est positif, on le décrémente pour arriver a 0

On a donc :

O ( n ) ou O ( x )

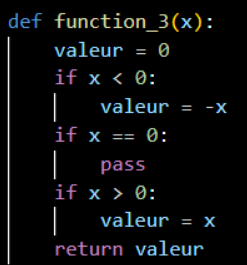
Cette fonction n'a pas de boucle donc elle ne ce répète pas.

On a donc :

O ( 1 )

Ex 3 - Algorithme de tri

• Créer un algorithme pour trier un tableau à N dimensions de M valeurs
• Chaque dimension doit être trié par ordre croissant de la somme des valeurs de la dimension inférieur
• Exemple pour un tableau à 2 dimensions de 3 valeurs [ [0,3,2], [9,4,5], [4,1,3] ] → [ [0,2,3], [1,3,4], [4,5,9] ]
• Calculer la complexité algorithmique de l’algorithme écrit

• la complecitée de ce programme est de O(n(m²+n))

def Trie_Tableau_Double(tab) : # complexitée O(n(m²+n))
    sorted_dico = {}

    print(tab[0])

            # n^(m+m*((m(m+1))/2))+n((m(m+1))/2)

    for sub_tab in tab :                                    # n
        val = 0
        sub_tab2 = []
        for elt in sub_tab :                                # m
            val += elt

        for i in range(len(sub_tab)):                       # m
            if i == 0 :
                sub_tab2.append(sub_tab[i])
            else : 
                for j in range(len(sub_tab2)+1):            # (m(m+1))/2
                    if j >= len(sub_tab2):
                        sub_tab2.append(sub_tab[i])
                    else : 
                        if sub_tab[i] <= sub_tab2[j] :
                            sub_tab2.insert(j,sub_tab[i])
                            break
        
        sorted_dico[val] = sub_tab2
    
    tab = []
    index_tab = []

            # n*(m(m+1))/2

    for clef,valeur in sorted_dico.items() :                # n
        if index_tab == [] :
            tab.append(valeur)
            index_tab.append(clef)
        else : 
            for j in range(len(index_tab)+1):               # (m(m+1))/2
                    if j >= len(index_tab):
                        tab.append(valeur)
                        index_tab.append(clef)
                    else : 
                        if clef <= index_tab[j] :
                            tab.insert(j,valeur)
                            index_tab.insert(j,clef)
                            break

    return tab

• la complecitée de ce programme est de O(n*m * log(m))

def Trie_Tableau_Double_bySort(tab) : # complexitée O(n*m * log(m))

   tab.sort()                  # n log(n)

   for sub_tab in tab :        # n
       sub_tab.sort()          # m log(m)
   
   return tab