SAE_S2.04/README.md

SAÉ S2.04 (visualisation de données)

La base de donnée que nous allons utiliser durant cette SAE se trouve se trouve dans le fichier data.csv

Pour chaque pays dans la base de donnée, on dispose des indicateurs suivants :

• Superficie (en milliers de km2)
• Population (en million)
• Taux de natalité (pour 1000 habitants)
• Taux de mortalité (pour 1000 habitants)
• Projection de la population en 2050 (en million)
• Taux de mortalité infantile (pour 1000 naissances)
• Indice de fécondité (enfants par femme)
• Proportion de moins de 15 ans (en pourcentage)
• Proportion de plus de 65 ans (en porcentage)
• Espérance de vie à la naissance pour les hommes
• Espérance de vie à la naissance pour les femmes
• Revenu national brut ppa par habitant (en dollars US)

Voici les indices (numéro de la ligne dans le fichier) des pays regroupés par continent :

Continent	Indice pays
Afrique	1 - 57
Amérique du nord	58 - 86
Amérique du sud	87 - 99
Asie	100 - 150
Europe	151 - 193
Océanie	194 - 207

Exercice 1

Question 1

Calculer la surface terrestre mondiale, le nombre d’habitants mondial et la densité moyenne d’habitants au km2.

Résultat :

• Surface terrestre mondiale : 133 950 670 km2
• Nombre d'habitants mondial : 7 534 720 000 habitants
• Densité moyenne d'habitants au km2 : 56.249961 habitants/km2

Question 2

Calculer la surface terrestre, le nombre d’habitants et la densité moyenne au km2 pour chaque continent.

Résultat :

• Afrique

  • Surface terrestre : 30 312 530 km2
  • Nombre d'habitants : 1 250 700 000 habitants
  • Densité moyenne d'habitants au km2 : 41.260165 habitants/km2

• Amérique du nord

  • Surface terrestre : 22 314 070 km2
  • Nombre d'habitants : 581 880 000 habitants
  • Densité moyenne d'habitants au km2 : 26.076821 habitants/km2

• Amérique du sud

  • Surface terrestre : 17 821 000 km2
  • Nombre d'habitants : 422 980 000 habitants
  • Densité moyenne d'habitants au km2 : 23.734919 habitants/km2

• Asie

  • Surface terrestre : 31 879 830 km2
  • Nombre d'habitants : 4 494 050 000 habitants
  • Densité moyenne d'habitants au km2 : 140.968443 habitants/km2

• Europe

  • Surface terrestre : 23 060 610 km2
  • Nombre d'habitants : 744 330 000 habitants
  • Densité moyenne d'habitants au km2 : 32.277117 habitants/km2

• Océanie

  • surface terrestre : 8 562 630 km2
  • Nombre d'habitants : 40 780 000 habitants
  • Densité moyenne d'habitants au km2 : 4.762555 habitants/km2

Question 3

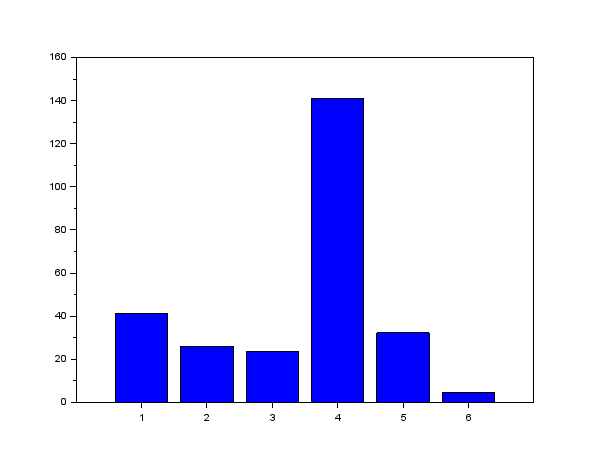
Représenter la densité moyenne d’habitants au km2 pour chaque continent en utilisant un diagramme en bâtons (on mettra en abscisse des entiers de 1 à 6).

Résultat :

Voici le diagramme en bâtons représentant la densité moyenne d’habitants au km2 pour chaque continent :

Avec le 1 qui représente l'Afrique, le 2 qui représente l'Amérique du nord, le 3 qui représente l'Amérique du sud, le 4 qui représente l'Asie, le 5 qui représente l'Europe et le 6 qui représente l'Océanie.

Question 4

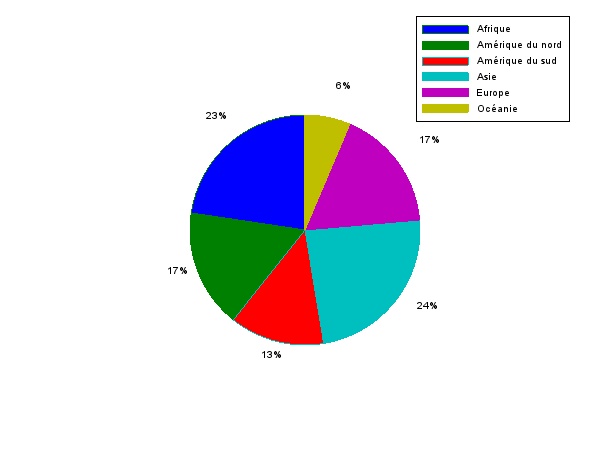
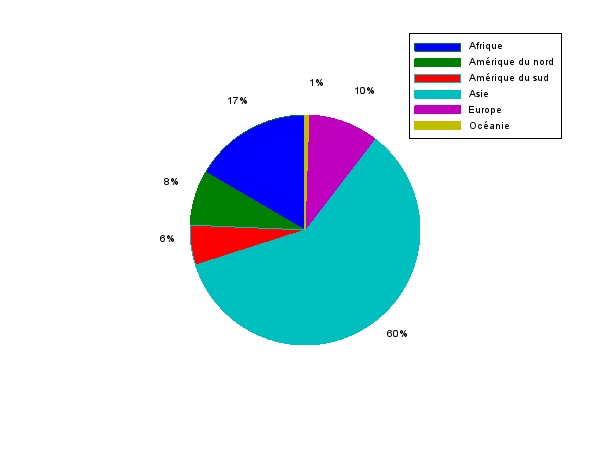
Représenter la répartition de la surface terrestre puis du nombre d'habitants par continent sous la forme de diagramme en camembert à l'aide de l'instruction pie.

Résultat :

Surface terrestre :

Population :

Exercice 2

On considère l’espérance de vie des hommes et des femmes par pays.

Question 1

Calculer la moyenne sur l’ensemble des pays. Ce résultat représente-t-il à l’espérance de vie mondiale des hommes (ou des femmes) ? pourquoi ? Comment l'estimer ?

Résultat :

• Moyenne de l'espérance de vie des hommes : 69 ans
• Moyenne de l'espérance de vie des femmes : 74 ans

Ce résultat ne représente pas correctement l'espérance de vie mondiale des hommes et des femmes car nous ne prenons pas en compte les pays qui ne possèdent pas de données sur l'espérance de vie des hommes et des femmes, ce qui veut dire que dans le calcule nous n'avons pas tous le pays, notamment Andorre.

Pour estimer la moyenne de l'espérance de vie mondiale des hommes et des femmes il faut prendre en compte les pays qui ne possèdent pas de données sur l'espérance de vie. Pour cela, il faut calculer la moyenne de l'espérance de vie des hommes et des femmes pour chaque pays et ensuite calculer la moyenne de ces moyennes.

Question 2

Calculer la médiane, la variance et l’écart-type.

Résultat :

• Homme

  • Médiane de l'espérance de vie des hommes : 71
  • Variance de l'espérance de vie des hommes : 58.328141
  • Ecart-type de l'espérance de vie des hommes : 7.637286

• Femme

  • Médiane de l'espérance de vie des femmes : 77
  • Variance de l'espérance de vie des femmes : 68.388844
  • Ecart-type de l'espérance de vie des femmes : 8.269755

Question 3

Calculer les esprérances de vie minimale et maximale en précisant les pays correspondant à ces valeurs.

Résultat :

• Homme

  • L'espérence de vie minimale des hommes : 50 ans
    • Ce qui correspond au pays : Centrafricaine(République)
  • L'espérence de vie maximale des hommes : 85 ans
    • Ce qui correspond au pays : Saint-Marin

• Femme

  • L'espérence de vie minimale des femmes : 52 ans
    • Ce qui correspond au pays : SierraLeone
  • L'espérence de vie maximale des femmes : 89 ans
    • Ce qui correspond au pays : Saint-Marin

Question 4

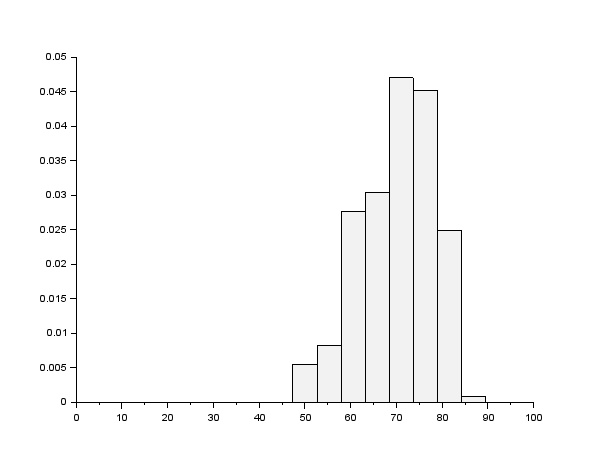
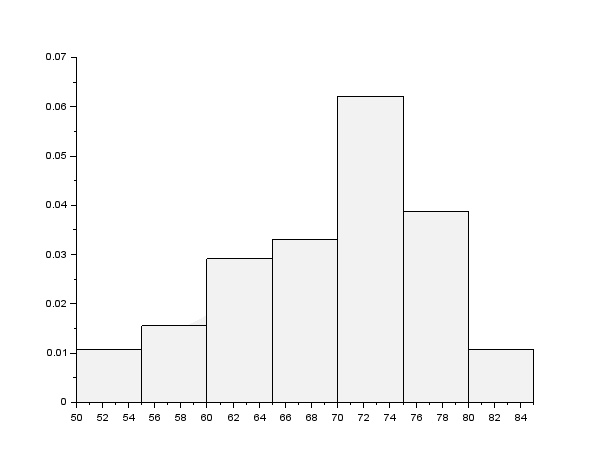
Représenter l’histogramme de l’espérance de vie des hommes par pays sur l’intervalle [0, 100] avec 20 classes. Quelle est la classe modale de l’espérance de vie des hommes par pays ?

Résultat :

• Histogramme de l'espérance de vie des hommes par pays sur l'intervalle [0, 100] avec 20 classes

Nous pouvons voir que la classe modale est celle entre 70 et 75 ans, c'est à dire la classe 5. Mais nous manquons de précision, nous allons donc affiner l'histogramme.

• Histogramme de l'espérance de vie des hommes par pays sur l'intervalle [50, 85] avec 8 classes

Ici nous pouvons voir avec plus de précision que la classe modale est celle entre 70 et 75 ans, c'est à dire la classe 5.

Question 5

Classer les pays suivant les valeurs croissantes de la colonne homme. En déduire le pays où l’espérance de vie des hommes est la plus grande et celui où elle est la plus petite.

Résultat :

• Pays où l'espérance de vie des hommes est la plus grande : Saint-Marin
• Pays où l'espérance de vie des hommes est la plus petite : Centrafricaine(République)

Question 6

Déterminer les valeurs du premier et du troisième quartile ainsi que l’écart inter-quartile de la colonne homme. En déduire la liste des pays dont l’espérance de vie est inférieure au premier quartile.

Résultat : La liste des pays dont l’espérance de vie est inférieure au premier quartile est :

• Centrafricaine(République)
• SierraLeone
• Tchad
• Lesotho
• Côted'Ivoire
• Nigeria
• Somalie
• Swaziland
• Guinée-Bissau
• Burundi
• Sud-Soudan
• Mozambique
• Gabon
• Mali
• Cameroun
• Angola
• Congo
• Congo(Répdémdu)
• Bénin
• BurkinaFaso
• Guinée
• Niger
• Togo
• Zambie
• Zimbabwe
• Gambie
• Malawi
• Ghana
• Liberia
• Djibouti
• AfriqueduSud
• Haïti
• Mauritanie
• Comores
• Érythrée
• Ouganda
• Namibie
• Afghanistan
• Soudan
• Éthiopie
• Tanzanie
• Botswana
• Yémen
• Guam
• Nouvelle-Zélande

Question 7

Donner les valeurs du premier et du neuvième décile ainsi que la liste des pays dont l'espérance de vie est inférieure au premier décile ou supérieure au neuvième décile. Donner leur répartition suivant les continents.

Résultat : La liste des pays dont l'espérance de vie est inférieure au premier décile ou supérieure au neuvième décile est :

• Centrafricaine(République)
• SierraLeone
• Tchad
• Lesotho
• Côted'Ivoire
• Nigeria
• Somalie
• Swaziland
• Guinée-Bissau
• Burundi
• Sud-Soudan
• Mozambique
• Gabon
• Mali
• Cameroun
• Angola
• Congo
• Congo(Répdémdu)
• Chypre
• Israël
• Chine-Macao
• Pays-Bas
• Croatie
• Macédoine
• Slovénie
• Nouvelle-Calédonie
• Singapour
• Chine-HongKong
• Japon
• Islande
• Norvège
• Suède
• Liechtenstein
• Luxembourg
• Suisse
• Grèce
• Portugal

La répartition des pays suivant les continents est :

• Afrique :

  • Centrafricaine(République)
  • SierraLeone
  • Tchad
  • Lesotho
  • Côted'Ivoire
  • Nigeria
  • Somalie
  • Swaziland
  • Guinée-Bissau
  • Burundi
  • Sud-Soudan
  • Mozambique
  • Gabon
  • Mali
  • Cameroun
  • Angola
  • Congo
  • Congo(Répdémdu)

• Asie :

  • Chypre
  • Israël
  • Chine-Macao
  • Singapour
  • Chine-HongKong
  • Japon

• Europe :

  • Pays-Bas
  • Croatie
  • Macédoine
  • Slovénie
  • Islande
  • Norvège
  • Suède
  • Liechtenstein
  • Luxembourg
  • Suisse
  • Grèce
  • Portugal

• Océanie :

  • Nouvelle-Calédonie

Exercice 3

On rappelle que le taux d’accroissement naturel est la différence entre la natalité et la mortalité.

Question 1

Quels sont les accroissements minimaux et maximaux ?

Résultat :

• Le taux d'accroissement minimal est de 7 pour 1000.
• Le taux d'accroissement maximal est de 33 pour 1000.

Question 2

Faire afficher la liste des pays pour lesquels l’accroissement est négatif.

Résultat :

Les pays pour lesquels l'accroissement est négatif sont :

• Japon
• Estonie
• Lettonie
• Lituanie
• Allemagne
• Biélorussie
• Bulgarie
• Hongrie
• Roumanie
• Ukraine
• Bosnie-Herzégovine
• Croatie
• Grèce
• Italie
• Portugal
• Serbie

Question 3

Déterminer l’accroissement mondial moyen.

Résultat :

• Le taux d'accroissement mondial moyen est de 13,2 pour 1000.

Question 4

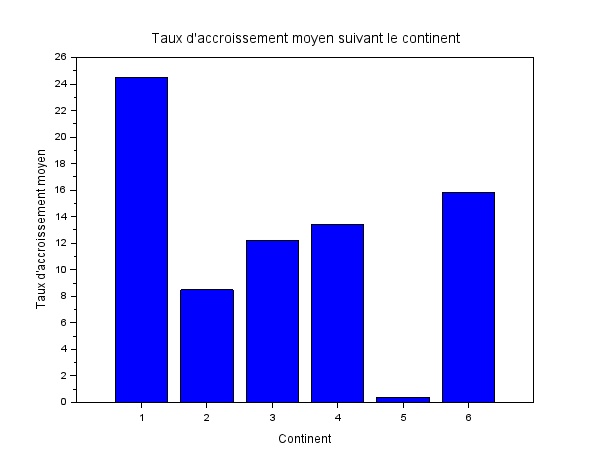
Faire un graphe de l'accroissement moyen suivant le continent.

Résultat :

Avec le 1 pour l'Afrique, le 2 pour l'Amérique du Nord, le 3 pour l'Amérique du Sud, le 4 pour l'Asie, le 5 pour l'Europe et le 6 pour l'Océanie.

Exercice 4

Question 1

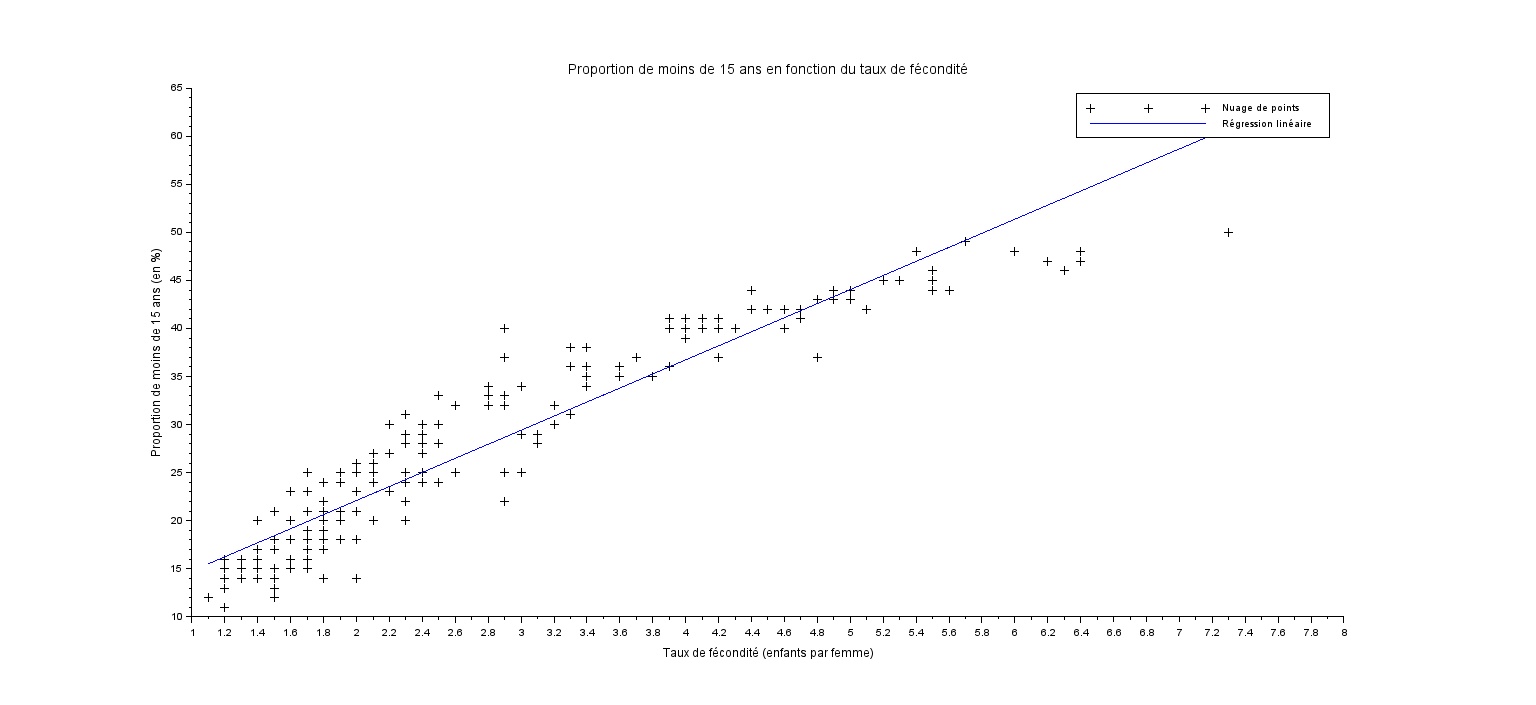
Afficher la proportion de moins de 15 ans en fonction du taux de fécondité. Essayer de caractériser au mieux la dépendance entre les deux quantités, en faisant une régression.

Résultat :

Question 2

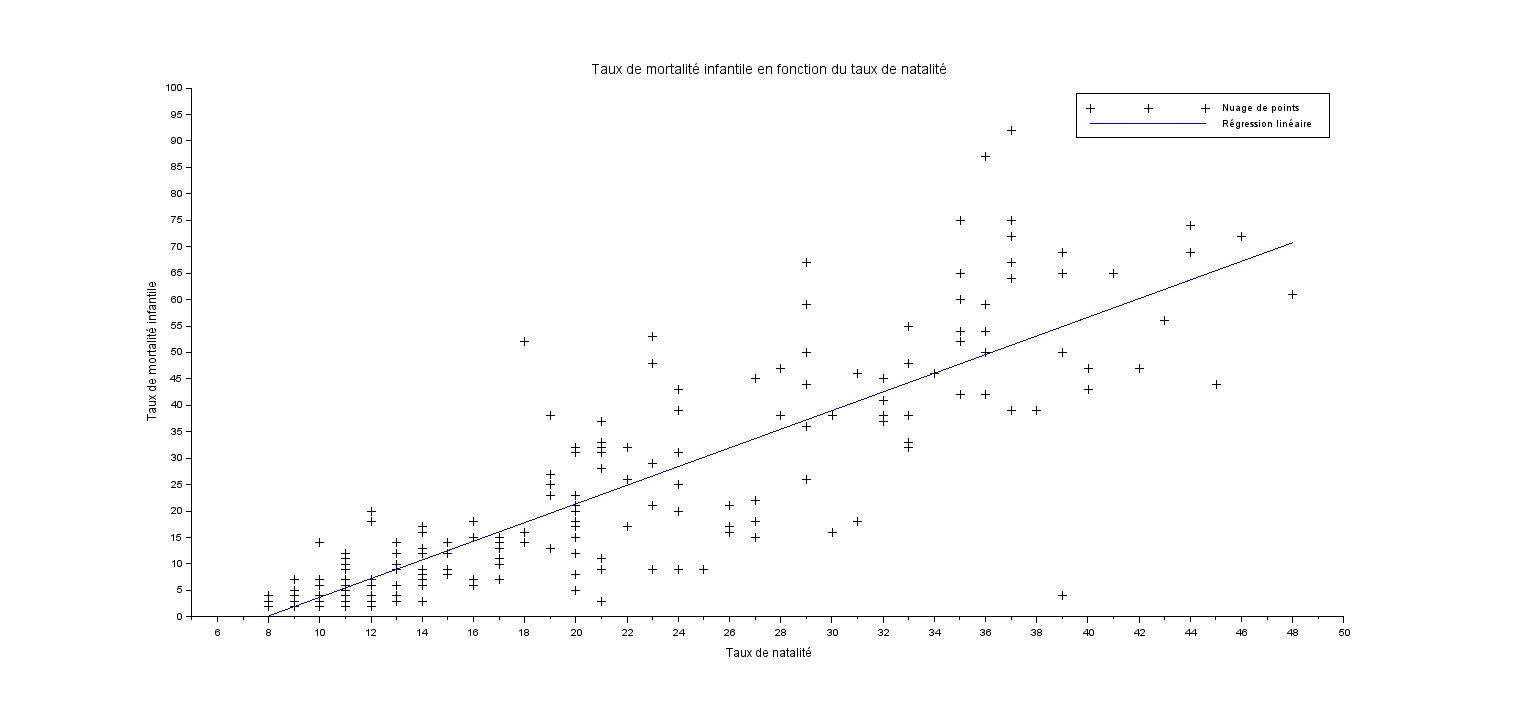
Afficher le taux de mortalité infantile en fonction du taux de natalité. Faites (et dessiner) une regression linéaire. Quel est le coefficient de corrélation ? Que peut-on dire ? Y'a-t-il une relation de causalité entre les deux ?

Résultat :

Le coefficient de corrélation est de 0.861870, ce qui est très proche de 1. Ce qui signifie qu'il y a une forte association positive entre les deux variables. On peut voir que la regression linéaire est très proche des points, ce qui confirme la forte association positive entre les deux variables. Nous pouvons alors dire qu'il y a une relation de causalité entre les deux, c'est à dire que le taux de natalité influe sur le taux de mortalité infantile, car si il y a plus de naissance, il y aura forcément plus de mortalité infantile.

Question 3

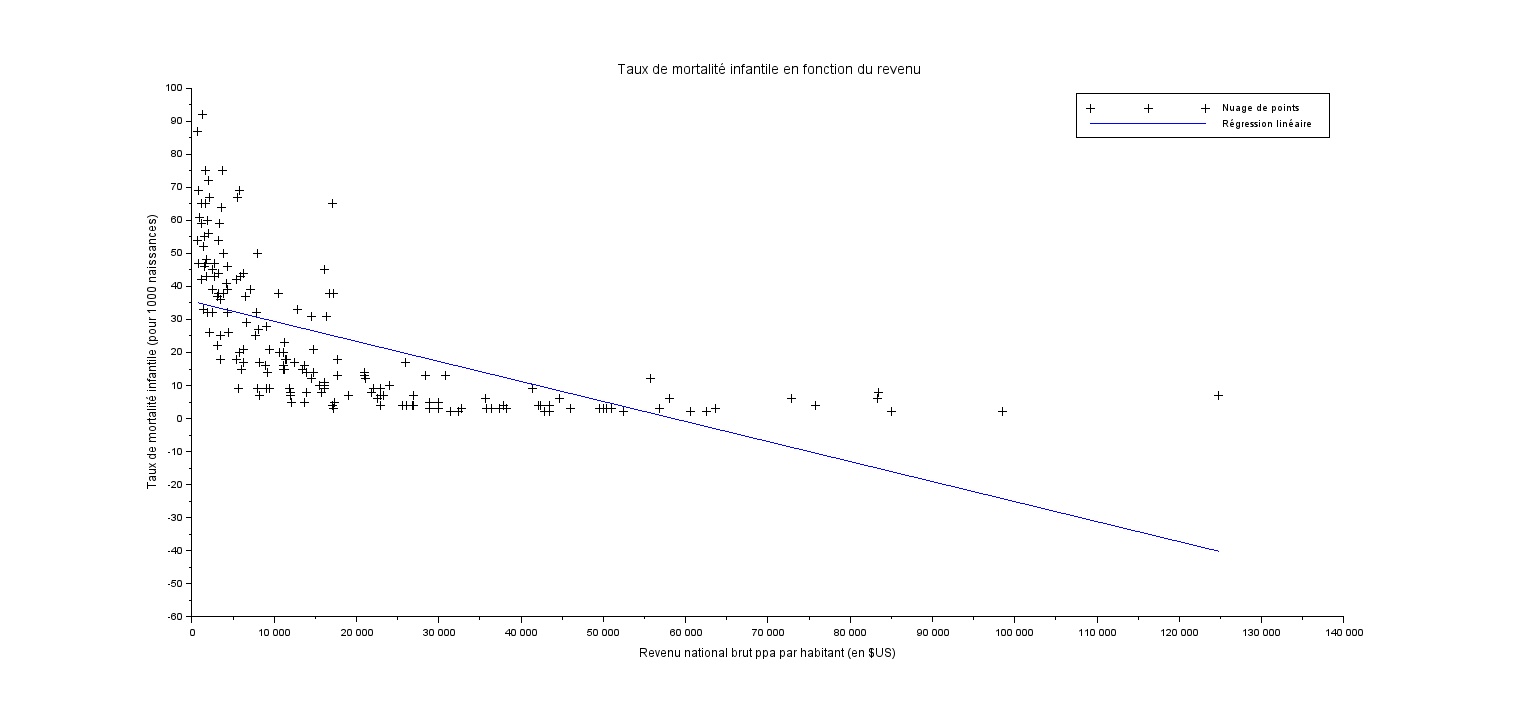
Afficher le taux de mortalité infantile en fonction du revenu. Calculez le coefficent de corrélation. Que peut-on dire ? Y'a-t-il une relation de causalité entre les deux.

Résultat :

Le coefficient de corrélation est de -0.604155, ce qui est plus proche de -1 que de 0. Nous pouvons alors dire que nous avons un assoication négative moyenne entre les deux variables. On peut aussi voir que la regression linéaire n'est pas très adaptée à ce nuage de points. Cependant, on peut dire qu'il y a une relation de causalité entre les deux variables, car plus le revenu est élevé, plus le taux de mortalité infantile est faible, et inversement.

[Question 4]

Cette dépendance vous semble-t-elle linéaire ? Comment la qualifiriez-vous ? Essayez de déterminer une relation mathématiques entre les deux.

Réponse :

La dépendance ne semble pas linéaire, mais plutôt exponentielle, nous pouvons notamment le voir avec la régression linéaire qui n'est pas du tout adaptée à cette situation. En effet, on peut voir que le taux de mortalité infantile diminue de manière exponentielle lorsque le revenu augmente. On peut alors dire que le taux de mortalité infantile est inversement proportionnel au revenu. On peut alors écrire la relation mathématique suivante : tauxMortaliteInfantile = a / revenu + b avec a et b des constantes.