Exercice 4 : Analyse des relations et dépendances
Table des matières
- Proportion de moins de 15 ans en fonction du taux de fécondité
- Taux de mortalité infantile en fonction du taux de natalité
- Taux de mortalité infantile en fonction du revenu
- Linéarité des dépendances
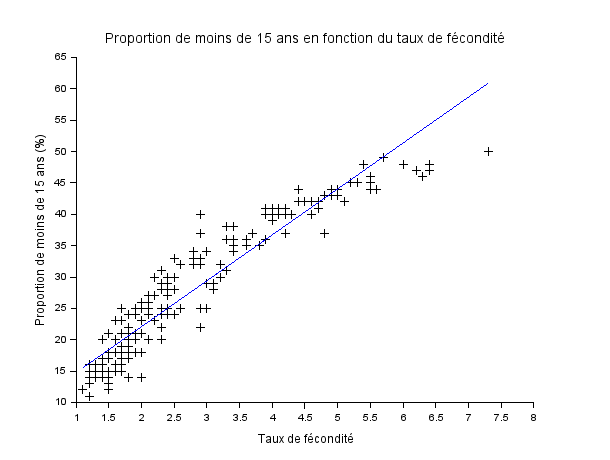
Question 1 : Proportion de moins de 15 ans en fonction du taux de fécondité
Afficher la proportion de moins de 15 ans en fonction du taux de fécondité. Essayer de caractériser au mieux la dépendance entre les deux quantités, en faisant une régression.
X = mtlb_t(data(:,8));
Y = mtlb_t(data(:,9));
plot2d(X,Y,-1);
[a,b] = reglin(X, Y);
plot(X,a*X+b);
Résultat :
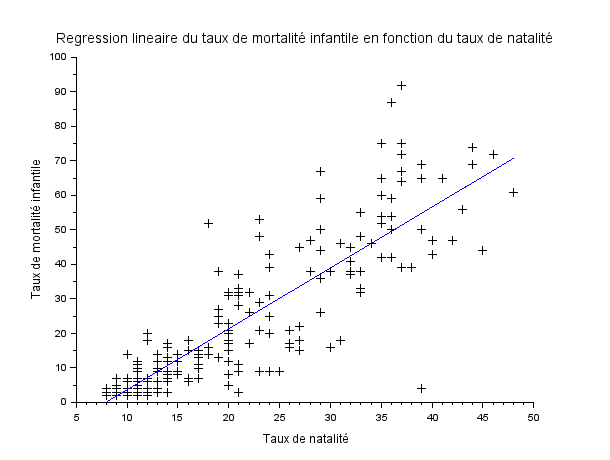
Question 2 : Taux de mortalité infantile en fonction du taux de natalité
Afficher le taux de mortalité infantile en fonction du taux de natalité. Faites (et dessiner) une regression linéaire. Quel est le coefficient de corrélation ? Que peut-on dire ? Y'a-t-il une relation de causalité entre les deux ?
X = mtlb_t(data(:,4));
Y = mtlb_t(data(:,7));
plot2d(X,Y,-1);
[a,b] = reglin(X, Y);
plot(X,a*X+b);
coefficient_correlation = correl(X,Y);
Résultat :
- Coefficient de correlation : 0.86
Le coefficient de correlation, qui est à l'image du graphe obtenu, nous montre qu'il y à une causalité entre les deux. PLus le taux de natalité est élevé plus le taux de mortalité infantile est élevé, ce qui est logique.
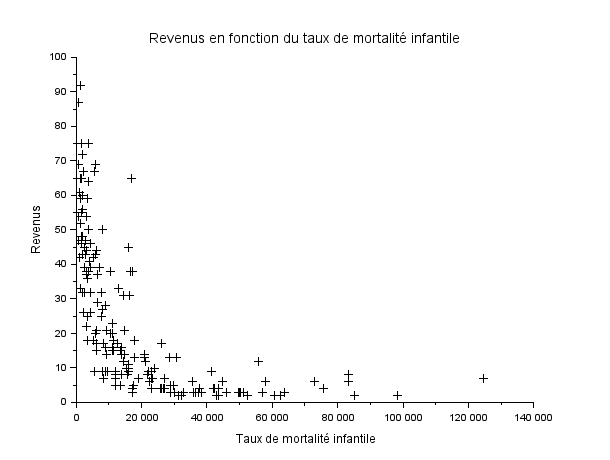
Question 3 : Taux de mortalité infantile en fonction du revenu
Afficher le taux de mortalité infantile en fonction du revenu. Calculez le coefficent de corrélation. Que peut-on dire ? Y'a-t-il une relation de causalité entre les deux.
X = find(data(:,13)>=0); // Revenus
XX = mtlb_t(data(X,13));
YY = mtlb_t(data(X,7));
plot2d(XX,YY,-1);
coefficient_correlation = correl(XX,YY)
Résultat :
- Coefficient de correlation : -0.60
On trouve donc une coefficient de correlation négatif de -60 globalement et cela montre un lien entre le revenus et le taux de martalité infantile, plus le revenus est élevé moins il y auras de mortalité infantile, ce qui est assez logique car un plus haut revenus sous entend un pays plus developpé.
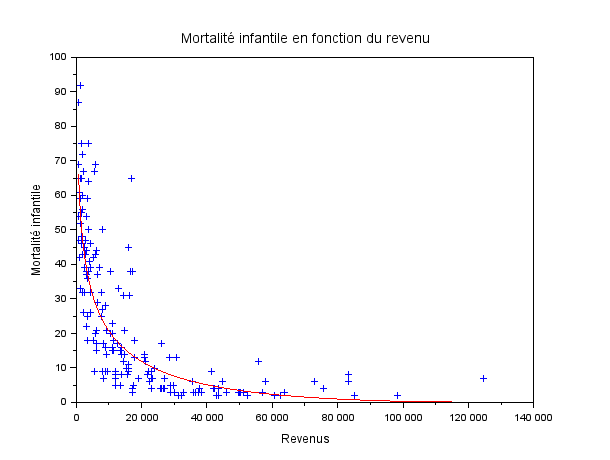
Question 4 : Linéarité des dépendances
Cette dépendance vous semble-t-elle linéaire ? Comment la qualifiriez-vous ? Essayez de déterminer une relation mathématiques entre les deux.
X = find(data(:,13)>=0);
mortalité_infantile = data(X,7);
revenu = data(X,13);
plot(revenu, mortalité_infantile,"+");
x=gsort(revenu);
[a, b]=reglin((revenu**0.1)', ((mortalité_infantile)**(0.5))');
coeff_correlation = correl(((revenu)**0.1), ((mortalité_infantile)**(0.5)));
plot(x, (a*x**0.1+b)**2, "r");
Résultat :
Après quelques essais, nous trouvons une relation de la forme suivante qui semble être la plus adaptée, avec une corrélation de -0.85 :
y^{0.5} = a \times x^{0.1} + b