7.2 KiB
7.2 KiB
Exercice 3 : Analyse des salaires
Table des matières
- Initialisation des variables
- Distribution des salaires par genre
- Histogramme des salaires moyens par niveau d'études
- Statistiques descriptives des salaires
- Répartition des salaires par genre
Initialisation des variables
Pour cette exercice, veuillez initaliser les variables suivantes :
csvDouble = csvRead("data.csv"); //ouvre data.csv en une matrice d'entier
csvString = csvRead("data.csv",[],[],'string'); //ouvre data.csv en une matrice de string
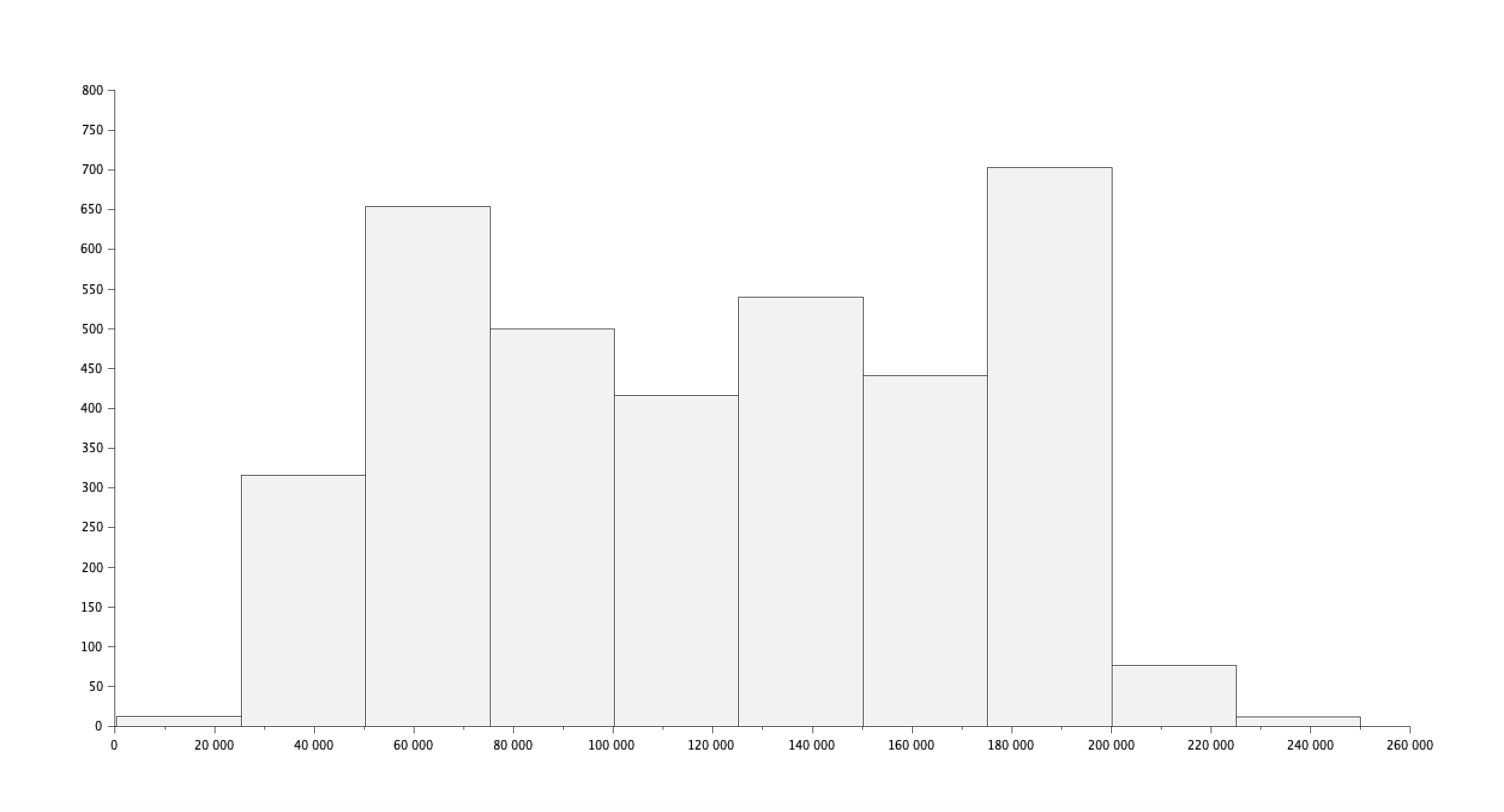
Question 1 : Distribution des salaires par genre
Donnez, sous forme d'histogramme, la distribution des salaires suivant le genre.
id_male = find(csvString(:,3) == "Male" );
salaire_male = csvDouble(id_male,7);
histplot(10,salaire_male,normalization=%f);
xlabel('Salaire');
ylabel('Effectifs');
title('Distribution des salaires pour les hommes');
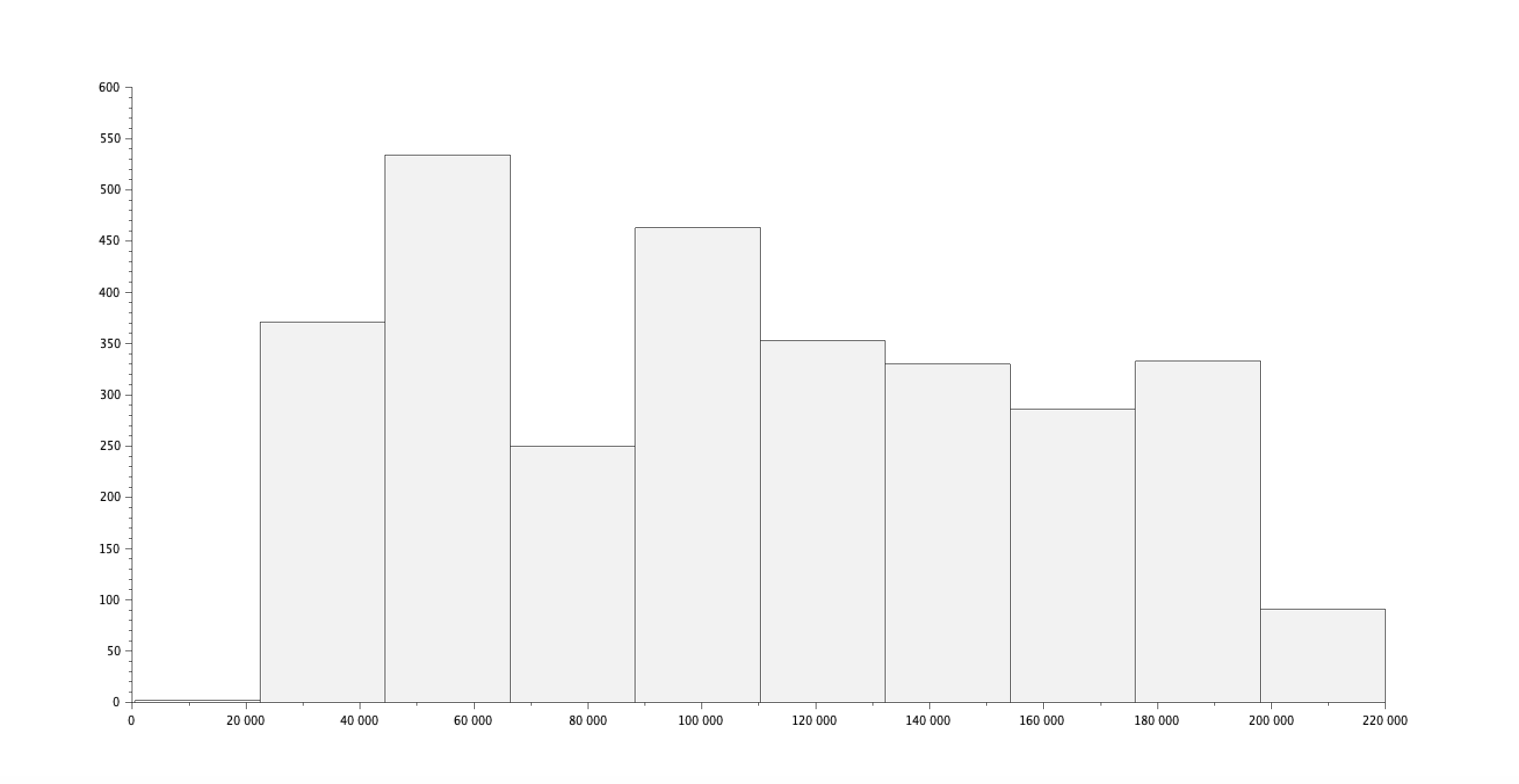
id_female = find(csvString(:,3) == "Female" );
salaire_female = csvDouble(id_female,7);
histplot(10,salaire_female,normalization=%f);
xlabel('Salaire');
ylabel('Effectifs');
title('Distribution des salaires pour les femmes');
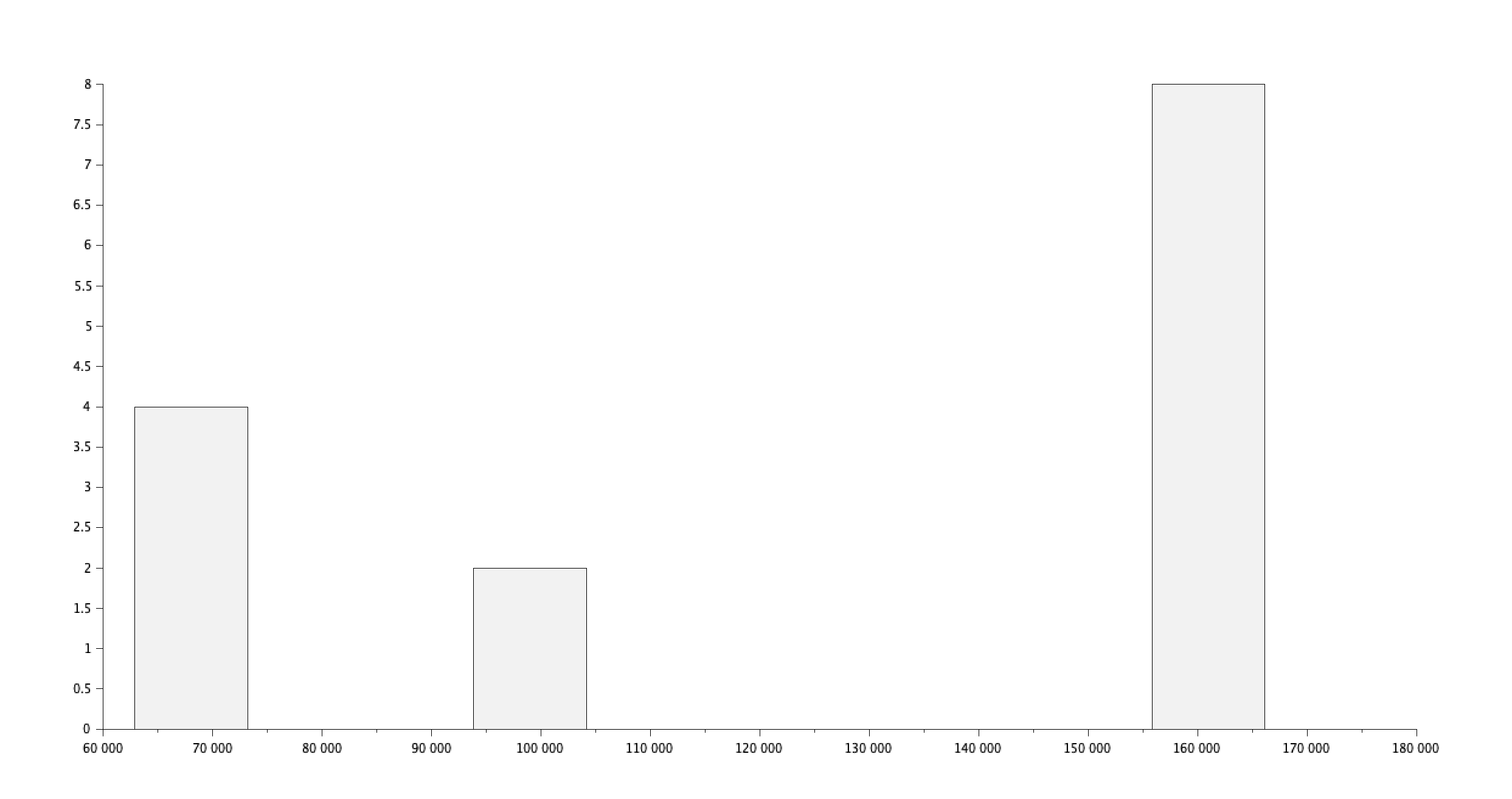
id_other = find(csvString(:,3) == "Other" );
salaire_other = csvDouble(id_other,7);
histplot(10,salaire_other,normalization=%f);
xlabel('Salaires');
ylabel('Effectifs');
title('Distribution des salaires pour les autres');
Résultat :
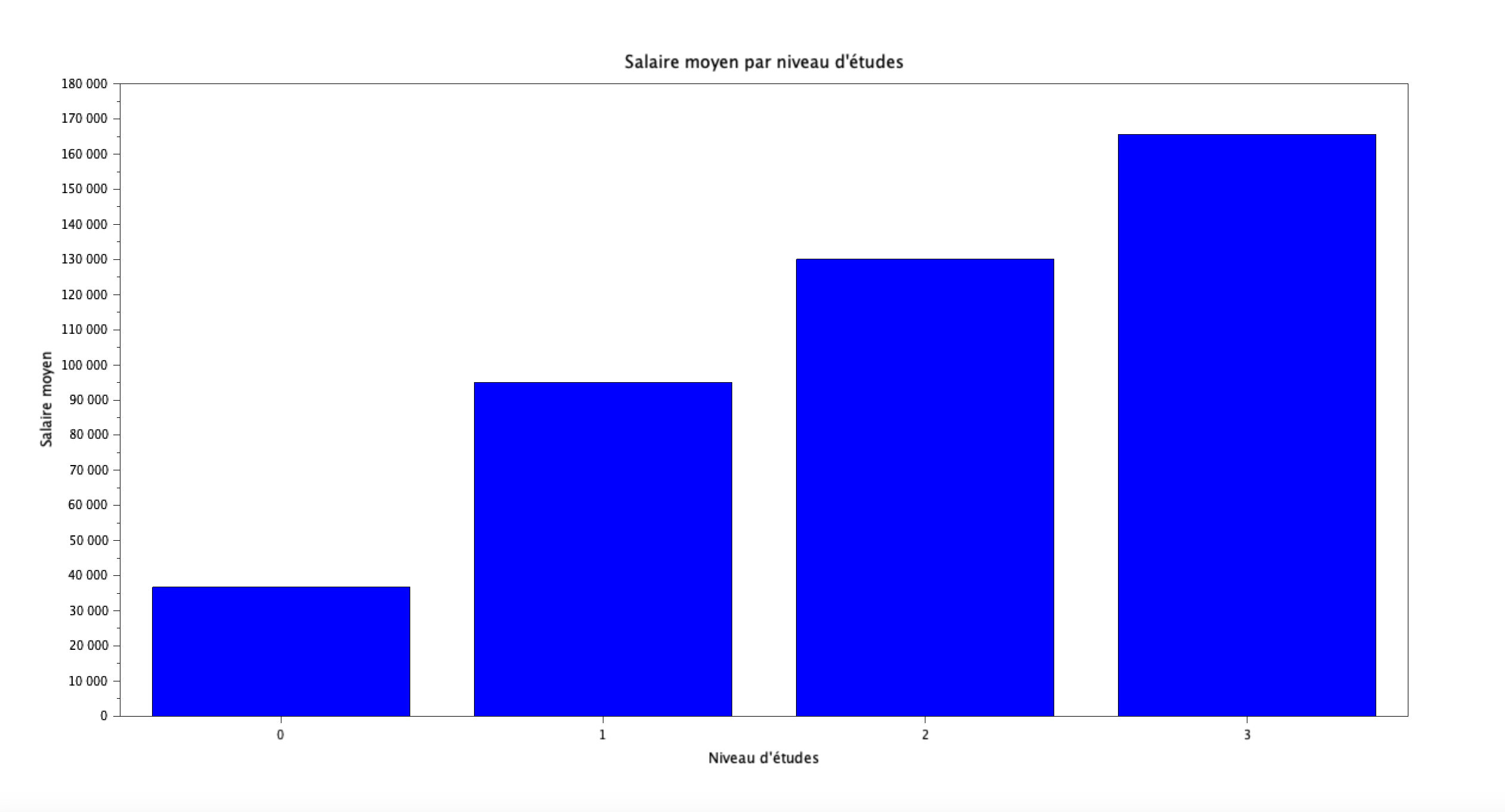
Question 2 : Histogramme des salaires moyens par niveau d'études
Tracez un histogramme des salaires moyens suivant le niveau d'études.
indice_high = find(csvDouble(:,4) == 0 );
salaire_high = csvDouble(indice_high,7);
moy_h = mean(salaire_high);
indice_b = find(csvDouble(:,4) == 1 );
salaire_b = csvDouble(indice_b,7);
moy_b = mean(salaire_b);
indice_m = find(csvDouble(:,4) == 2 );
salaire_m = csvDouble(indice_m,7);
moy_m = mean(salaire_m);
indice_p = find(csvDouble(:,4) == 3);
salaire_p = csvDouble(indice_p,7);
moy_p = mean(salaire_p);
matrice = [moy_h,moy_b,moy_m,moy_p];
bar([0,1,2,3],matrice);
xlabel("Niveau d''études");
ylabel("Salaire moyen");
title("Salaire moyen par niveau d''études");
Résultat :
Question 3 : Statistiques descriptives des salaires
Donnez les quartiles, interquartiles, minimum, maximum, moyenne, médiane, et écart-type des salaires. Tracez une boîte à moustaches.
mean(csvDouble(:,7)) //moyenne
min(csvDouble(:,7)) //min
max(csvDouble(:,7)) //max
median(csvDouble(:,7)) //médianne
quart(csvDouble(:,7)) //quartile
iqr(csvDouble(:,7)) //interquartile
stdev(csvDouble(:,7)) //ecart-type
sal = tabul(csvDouble(:,7));
[occurence_tri,indice_tri] = gsort(sal(:,2));
liste_exp = sal(:,1);
mode = liste_exp(indice_tri(1)) //mode
atomsLoad("stixbox");
boxplot(csvDouble(:,7),"orientation","horizontal");
xlabel('Salaires');
title('Boîte à moustache des salaires');
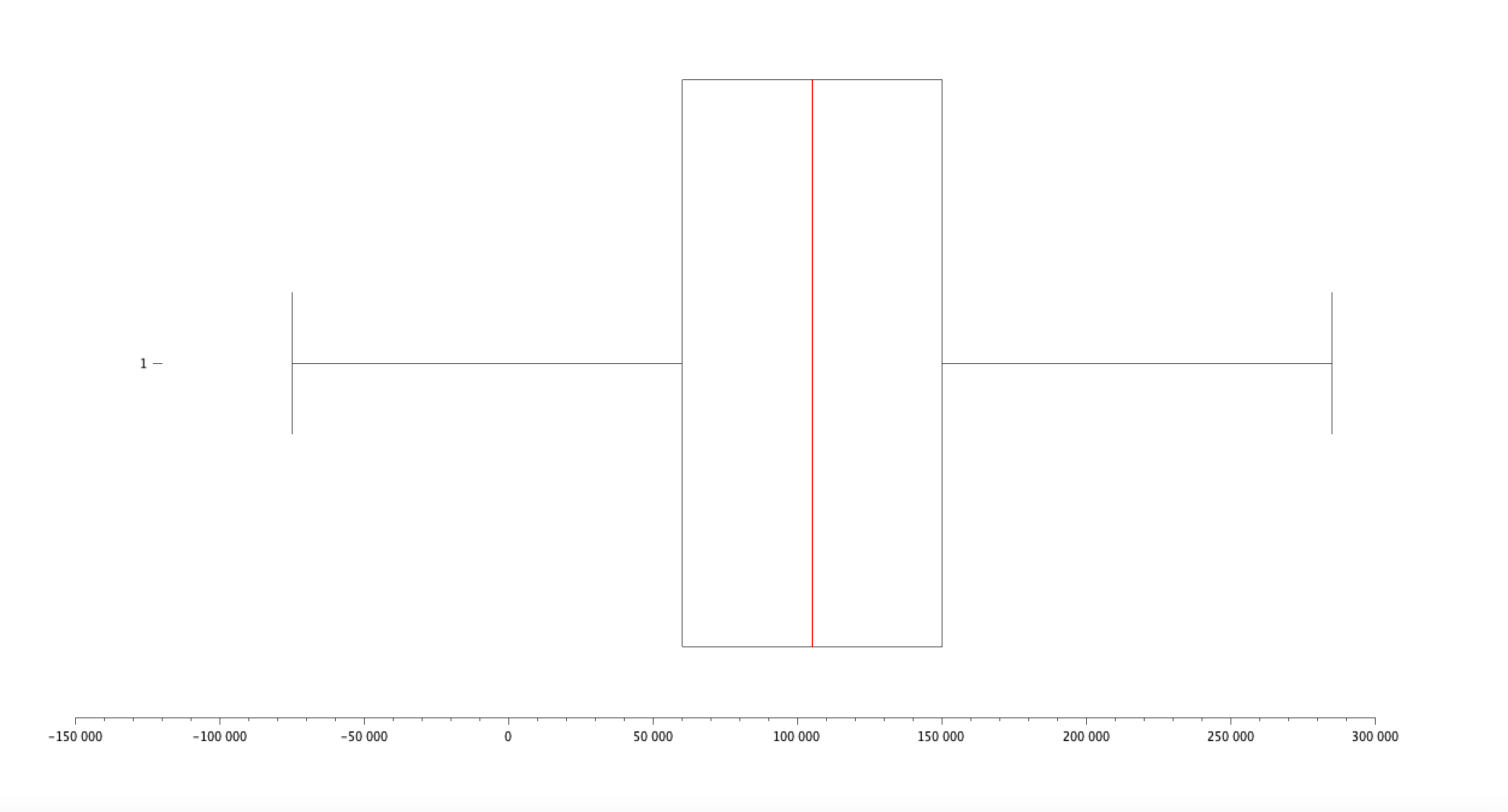
Résultat :
- Quartiles : [Q1, Q2 (médiane), Q3] = [70000, 115000, 160000]
- Interquartile Range (IQR) : Q(3) - Q(1) = 90000
- Minimum : 350
- Maximum : 250000
- Moyenne : 115326.96
- Médiane : 115000
- Mode : 140000
- Écart-type : 52786.184
Question 4 : Répartition des salaires par genre
Refaire la question précédente, en distinguant les genres. Tracez une boîte à moustache pour chaque genre. Commentaires ?
id_other = find(csvString(:,3) == "Other" )
salaire_other = csvDouble(id_other,7)
mean(salaire_other) //moyenne
min(salaire_other) //min
max(salaire_other) //max
median(salaire_other) //médianne
quart(salaire_other) //quartile
iqr(salaire_other) //interquartile
stdev(salaire_other) //ecart-type
sal = tabul(salaire_other);
[occurence_tri,indice_tri] = gsort(sal(:,2));
liste_sal = sal(:,1);
mode = liste_sal(indice_tri(1)) //mode
boxplot(salaire_other,"orientation","horizontal")
xlabel('Salaires');
title('Boîte à moustache des salaires des autres');
id_female = find(csvString(:,3) == "Female" )
salaire_female = csvDouble(id_female,7)
mean(salaire_female) //moyenne
min(salaire_female) //min
max(salaire_female) //max
median(salaire_female) //médianne
quart(salaire_female) //quartile
iqr(salaire_female) //interquartile
stdev(salaire_female) //ecart-type
sal = tabul(salaire_female);
[occurence_tri,indice_tri] = gsort(sal(:,2));
liste_sal = sal(:,1);
mode = liste_sal(indice_tri(1)) //mode
boxplot(salaire_female,"orientation","horizontal")
xlabel('Salaires');
title('Boîte à moustache des salaires des femmes');
id_male = find(csvString(:,3) == "Male" )
salaire_male = csvDouble(id_male,7)
mean(salaire_male) //moyenne
min(salaire_male) //min
max(salaire_male) //max
median(salaire_male) //médianne
quart(salaire_male) //quartile
iqr(salaire_male) //interquartile
stdev(salaire_male) //ecart-type
sal = tabul(salaire_male);
[occurence_tri,indice_tri] = gsort(sal(:,2));
liste_sal = sal(:,1);
mode = liste_sal(indice_tri(1)) //mode
boxplot(salaire_male,"orientation","horizontal")
xlabel('Salaires');
title('Boîte à moustache des salaires des hommes');
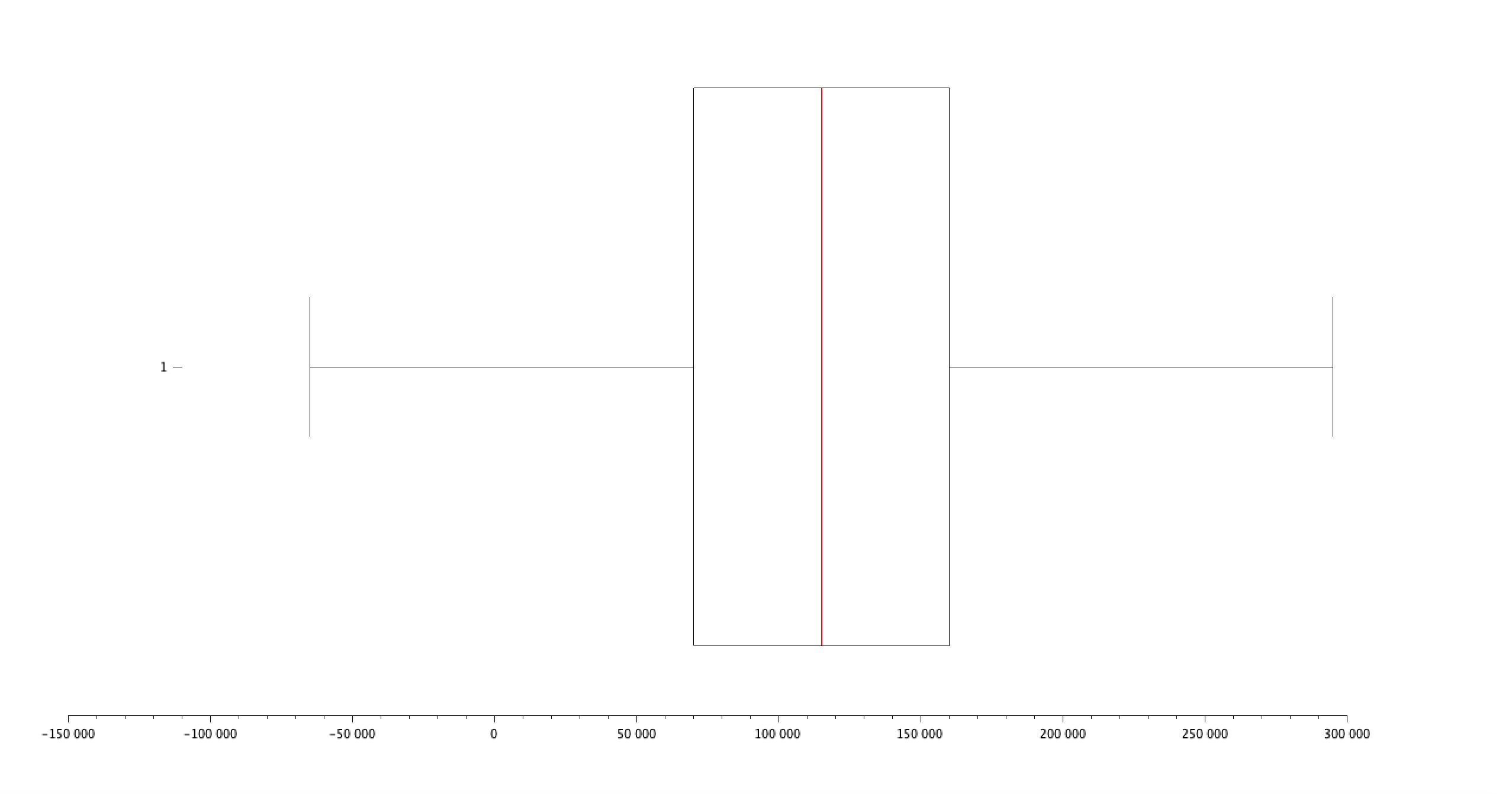
Résultat :
-
Hommes :
- Quartiles : [Q1, Q2 (médiane), Q3] = [75000, 120000, 170000]
- Interquartile Range (IQR) : QH(3) - QH(1) = 95000
- Minimum : 350
- Maximum : 250000
- Moyenne : 121389.87
- Médiane : 120000
- Écart-type : 52092.726
- Mode : 140000
-
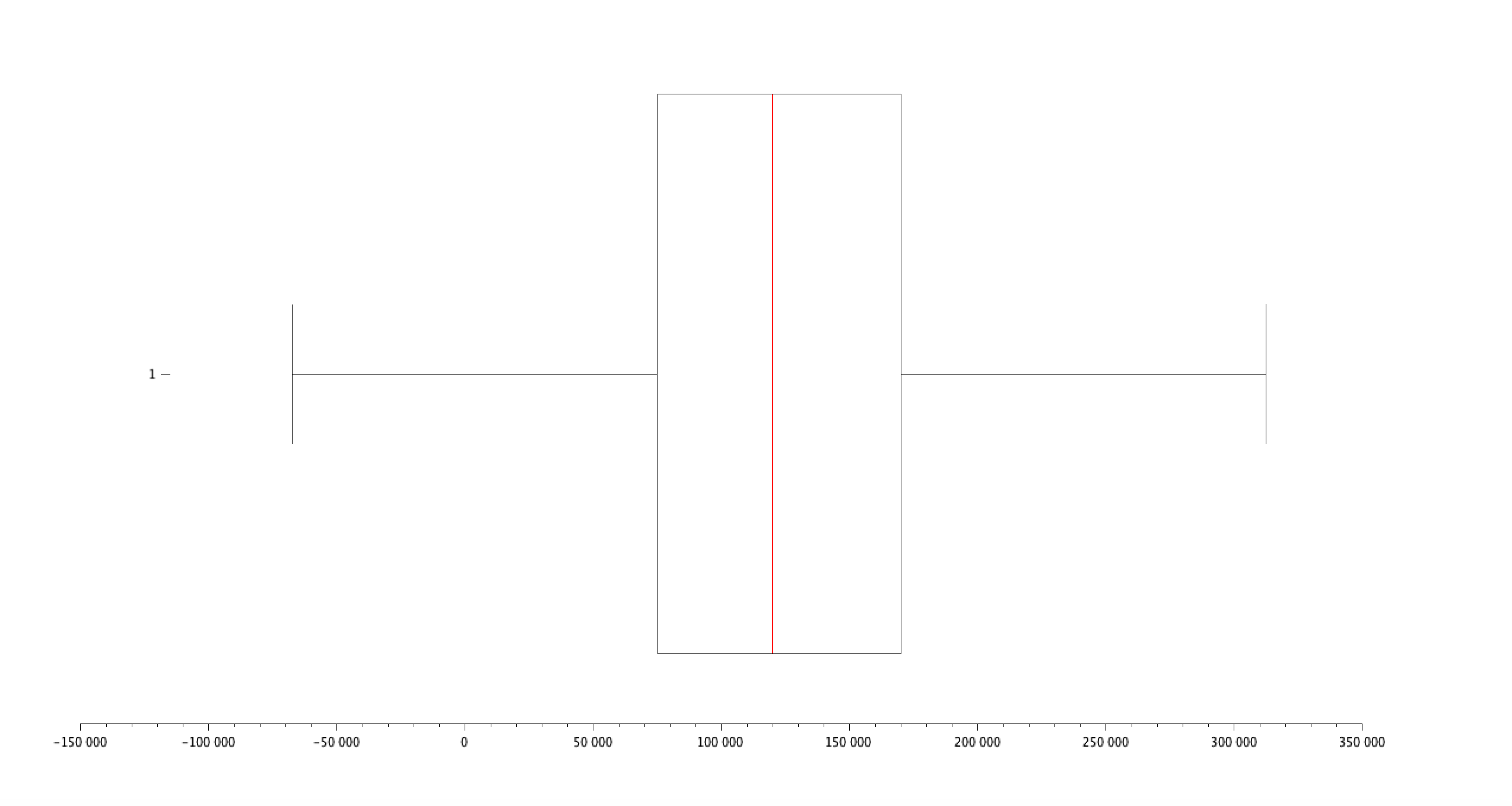
Femmes :
- Quartiles : [Q1, Q2 (médiane), Q3] = [60000, 105000, 150000]
- Interquartile Range (IQR) : QF(3) - QF(1) = 90000
- Minimum : 500
- Maximum : 220000
- Moyenne : 107889.00
- Médiane : 105000
- Écart-type : 52723.610
- Mode : 120000
-
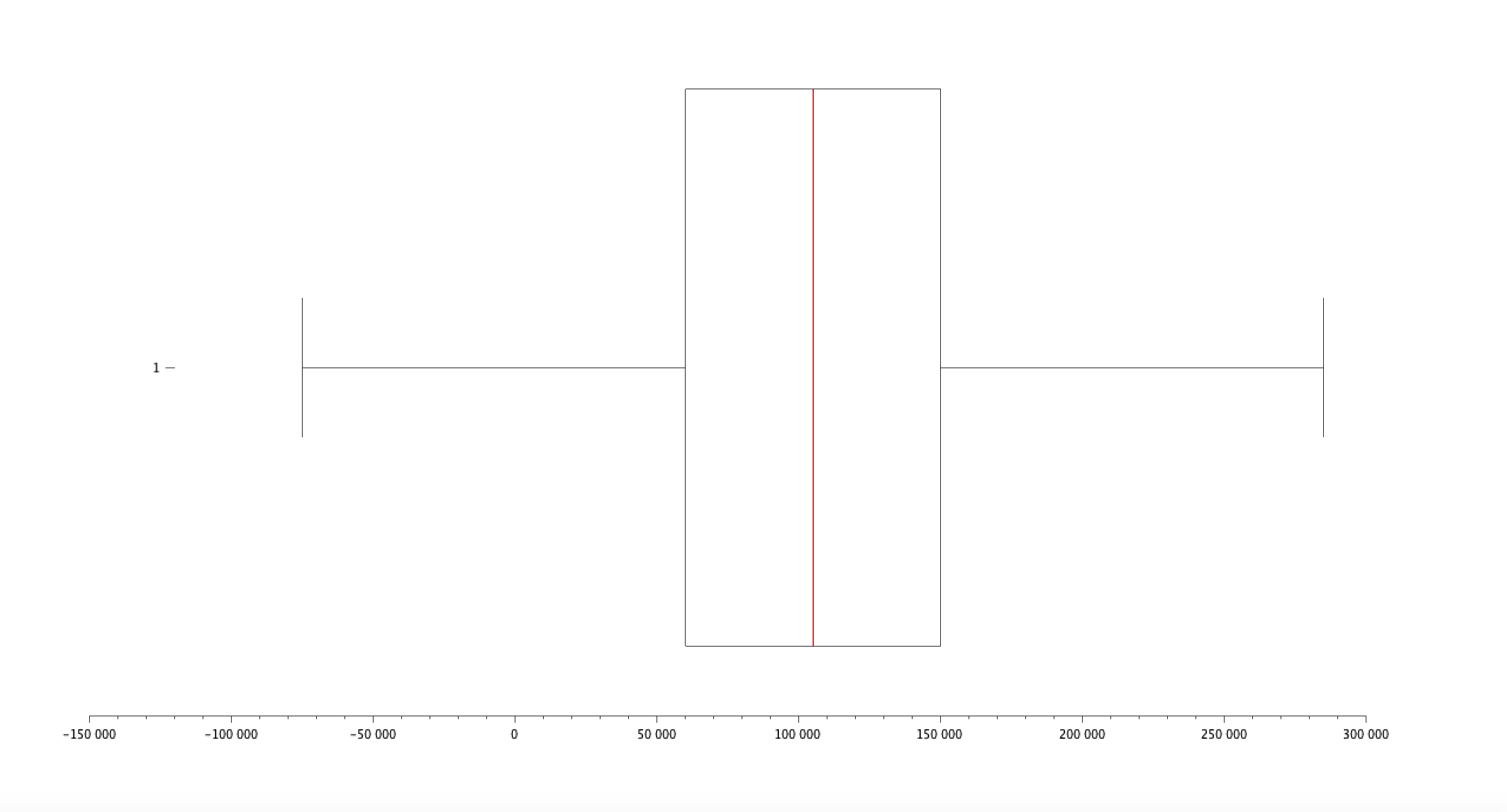
Autres :
- Quartiles : [Q1, Q2 (médiane), Q3] = [69032, 158610, 161393]
- Interquartile Range (IQR) : QF(3) - QF(1) = 92361
- Minimum : 62852
- Maximum : 166109
- Moyenne : 125869.86
- Médiane : 158610
- Écart-type : 44242.383
- Mode : 158966
-
Commentaires : Les 3 diagrammes moustaches sembles être très similaires. Le placement de la médiane et des quartiles se confondent.