| img | ||
| sources | ||
| .gitignore | ||
| Makefile | ||
| README.md | ||
Situation d'Apprentissage et d'Évaluation (Semestre 2) - Java
Sommaire
Rappel du sujet
L'algorithme d'Ariane
Ce projet a pour but d'étudier un algorithme de guidage, visant à conduire un objet mobile jusqu'à son but à travers un parcours d'obstacles. En hommage à la mythologie grecque, nous supposerons qu'il s'agit de Thésée, perdu dans le labyrinthe crétois, à la recherche de la sortie (on aurait pu aussi choisir une souris recherchant un morceau de fromage, ou un robot cherchant son point de ravitaillement).
Vous produirez un programme écrit en Java, sans emprunt extérieur (sauf l'API officielle), et accompagné d'un rapport. Le travail sera fait seul ou en binôme (un binôme est fortement recommandé, afin de vous permettre de vous familiariser avec les techniques de développement collaboratif), et devra être terminé avant le vendredi 28 avril 2023 à 23h59.
La partie logicielle sera développée dès le départ à l'aide du serveur Gitea du département. Le rapport prendra la forme d'un fichier au format PDF joint aux sources.
Principes généraux
Pour simplifier le problème, le labyrinthe sera représenté sous la forme d'une grille carrée. Chaque cellule de la grille peut être bloquée ou libre. La position initiale de Thésée ainsi que celle de la sortie pourront être placées sur n'importe quelles cases libres distinctes.
À chaque étape de la simulation, Thésée a quatre options :
- se déplacer d'une case vers le nord,
- se déplacer d'une case vers le sud,
- se déplacer d'une case vers l'est,
- se déplacer d'une case vers l'ouest.
Ce mouvement peut avoir trois conséquences :
- la case de destination est bloquée (et Thésée n'a donc pas changé de case),
- la case de destination est libre (et Thésée s'y est rendu),
- la case de destination est la sortie (et la simulation est terminée).
L'algorithme que vous devez écrire dictera à Thésée son prochain déplacement à chaque étape.
Fonctionnalités demandées
Le programme se déroulera en trois parties : choix de la grille, choix de l'algorithme, puis test de l'algorithme.
- Pour choisir la grille, l'utilisateur pourra charger une grille existante (en sélectionnant un fichier au format approprié à l'aide d'un JFileChooser) ou construire une nouvelle grille.
S'il choisit cette dernière option, l'utilisateur décidera d'abord de la taille de la grille. Il pourra ensuite partir d'une grille vide, ou d'une grille remplie aléatoirement. Il sera alors capable de modifier individuellement l'état de chaque case, puis décidera de la position initiale de Thésée et de la sortie.
Une fois la grille terminée, l'utilisateur aura la possibilité de la sauvegarder. Vous pouvez ici aussi employer un JFileChooser pour donner à l'utilisateur le choix de l'emplacement et du nom de la sauvegarde. - L'utilisateur pourra ensuite choisir entre deux algorithmes : l'un, totalement aléatoire (chaque direction a autant de chances d'être choisie), et l'autre déterministe.
Ce dernier devra baser ses décisions uniquement sur les coordonnées actuelles de Thésée et sur sa mémoire des conséquences de ses actions précédentes. Il n'aura aucune connaissance préalable de l'emplacement des cases obstruées ou de la sortie. - Une fois l'algorithme et la grille choisie, l'utilisateur devra sélectionner une visualisation du déroulement de la simulation : manuelle ou automatique.
Dans le mode manuel, l'avancement de Thésée sera représenté sur la grille, et le choix préconisé par l'algorithme pour la prochaine étape sera affiché. L'utilisateur fera défiler les étapes en appuyant sur une touche (capturée par un KeyListener), jusqu'à la fin de la simulation. Ce mode sert à voir en détail le comportement de l'algorithme.
Dans le mode automatique, la grille n'est pas affichée, et la simulation est effectuée sans intervention de l'utilisateur. On affichera seulement le nombre d'étapes nécessaires pour compléter la simulation. Dans le cas de l'algorithme aléatoire, on fera tourner la simulation 100 fois avant d'afficher le nombre d'étapes moyen (puisque le résultat sera différent à chaque simulation).
Vous vous efforcerez d'écrire l'algorithme déterministe le plus efficace possible. Il devra impérativement être capable de trouver la sortie si un chemin existe (vous devrez en fournir la preuve dans le rapport), et ses performances (en termes de nombre d'étapes nécessaires pour trouver la sortie) devront être visiblement meilleures que celles de l'algorithme aléatoire.
Toutes les interactions devront impérativement être en mode graphique. Les seuls affichages permis à la console sont les messages envoyés à la sortie sur erreur afin de documenter les problèmes rencontrés.
Format de sauvegarde des grilles
Le fichier ne contiendra pas de texte. Le premier octet servira à stocker la taille de la grille. Le second et le troisième stockeront respectivement les numéros de ligne et de colonne de la position initiale de Thésée, le quatrième et le cinquième octet jouant le même rôle pour la position de la sortie.
A partir de ce point, chaque bit représente l'état d'une case : 0 si elle est libre, ou 1 si elle est bloquée. La grille est ainsi décrite colonne par colonne.
Exemple :
Cette grille correspond au fichier suivant :
Vous pouvez télécharger ce fichier pour tester votre programme.
Rapport
Makefile
make runcompile et exécute le programmemake docgénère et ouvre la documentationmake cleansupprime les exécutables et la documentation
Déroulement du programme
Menu d'accueil
Après avoir exécuté le programme, l'application ouvre une fenêtre contenant le premier menu : le menu d'accueil.
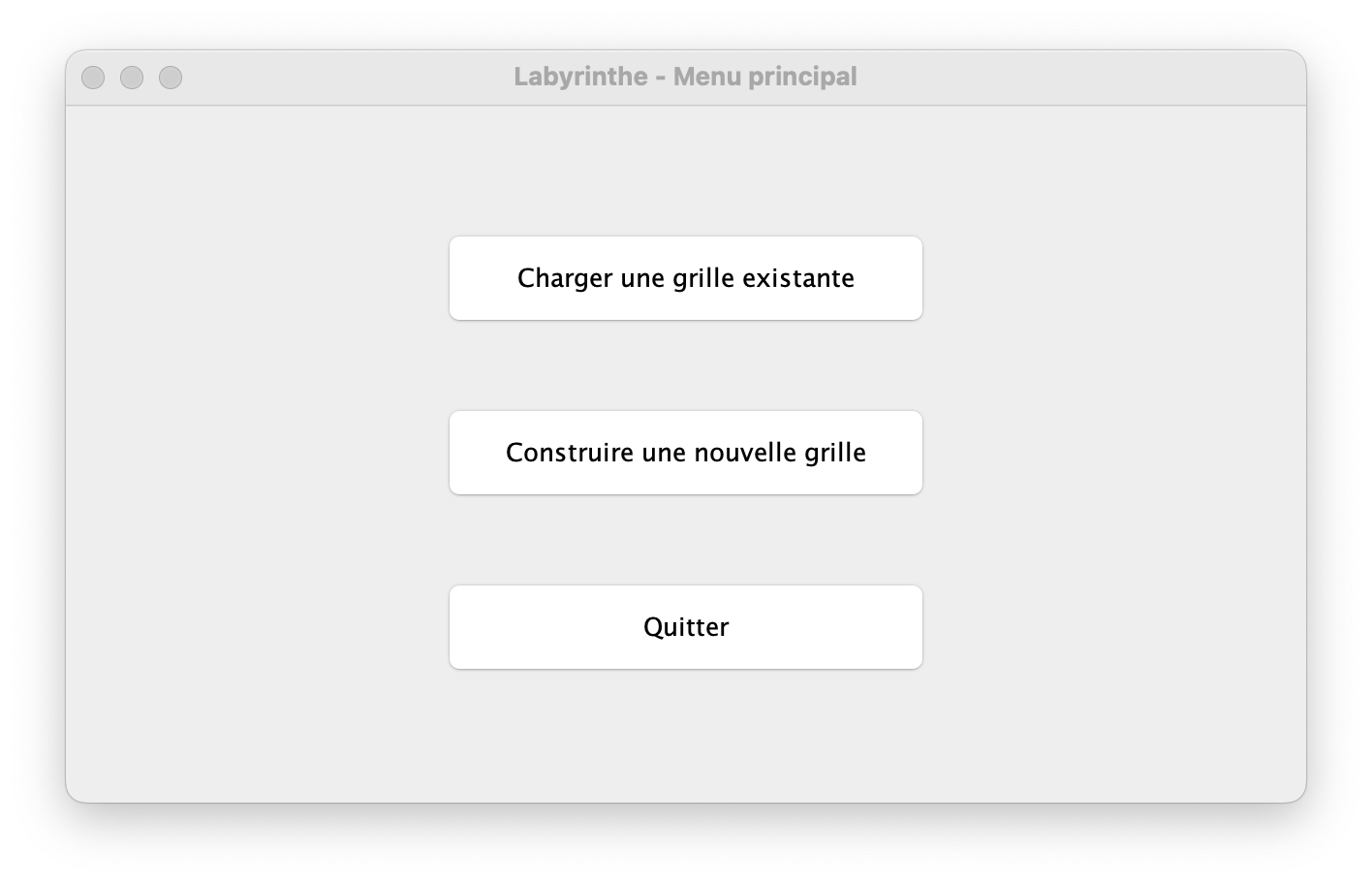
On a alors 3 possibilités :
- charger une grille existante ;
- construire une nouvelle grille ;
- quitter.
La première possibilité permet de charger un fichier .lab contenant la sauvegarde d'une grille, ce qui nous dirige directement vers le menu de modification. À noter qu'on vérifie scrupuleusement le contenu du fichier pour vérifier sa compatibilité. Il est impossible de charger un fichier qui n'est pas au bon format, même si son extension est .lab.
La deuxième redirige vers le menu d'initialisation qu'on verra juste après.
Enfin, la troisième possibilité quitte simplement le programme en fermant l'application.
Menu d'initialisation
En choisissant la deuxième option, l'application ouvre le menu d'initialisation d'une nouvelle grille. On peut alors choisir la taille de celle-ci via le slider, entre 3x3 et 20x20 (10x10 par défaut), et si l'on veut partir d'une grille totalement vide ou remplie aléatoirement à 50 %.
Menu de modification
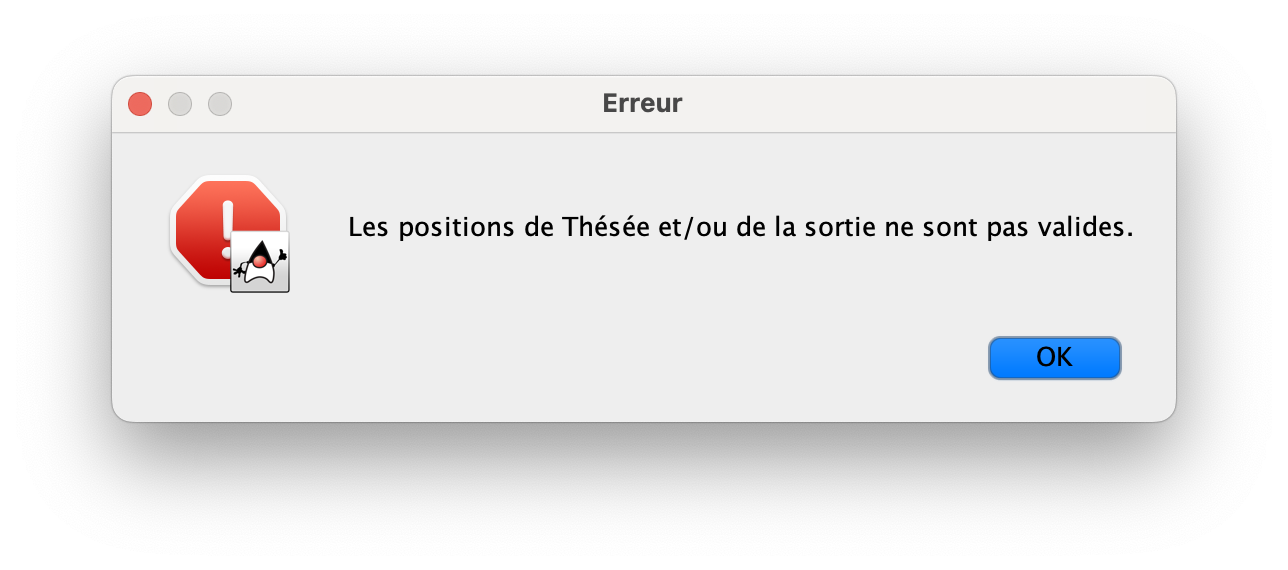
Une fois la grille initialisée, on passe maintenant à sa modification. On peut modifier l'état de la grille case par case en cliquant sur cette dernière. Il y a sur le panneau gauche deux boutons que l'on peut activer et désactiver s'il on veut placer Thésée ou la sortie.
Une fois les modification apportée, on a la possibilité de la sauvegarder ou de passer directement à la simulation.
Menu de simulation
Maintenant qu'on a notre grille, on a le choix entre les deux algorithmes : aléatoire ou déterministe, mais aussi entre les deux visualisations : manuelle ou automatique.
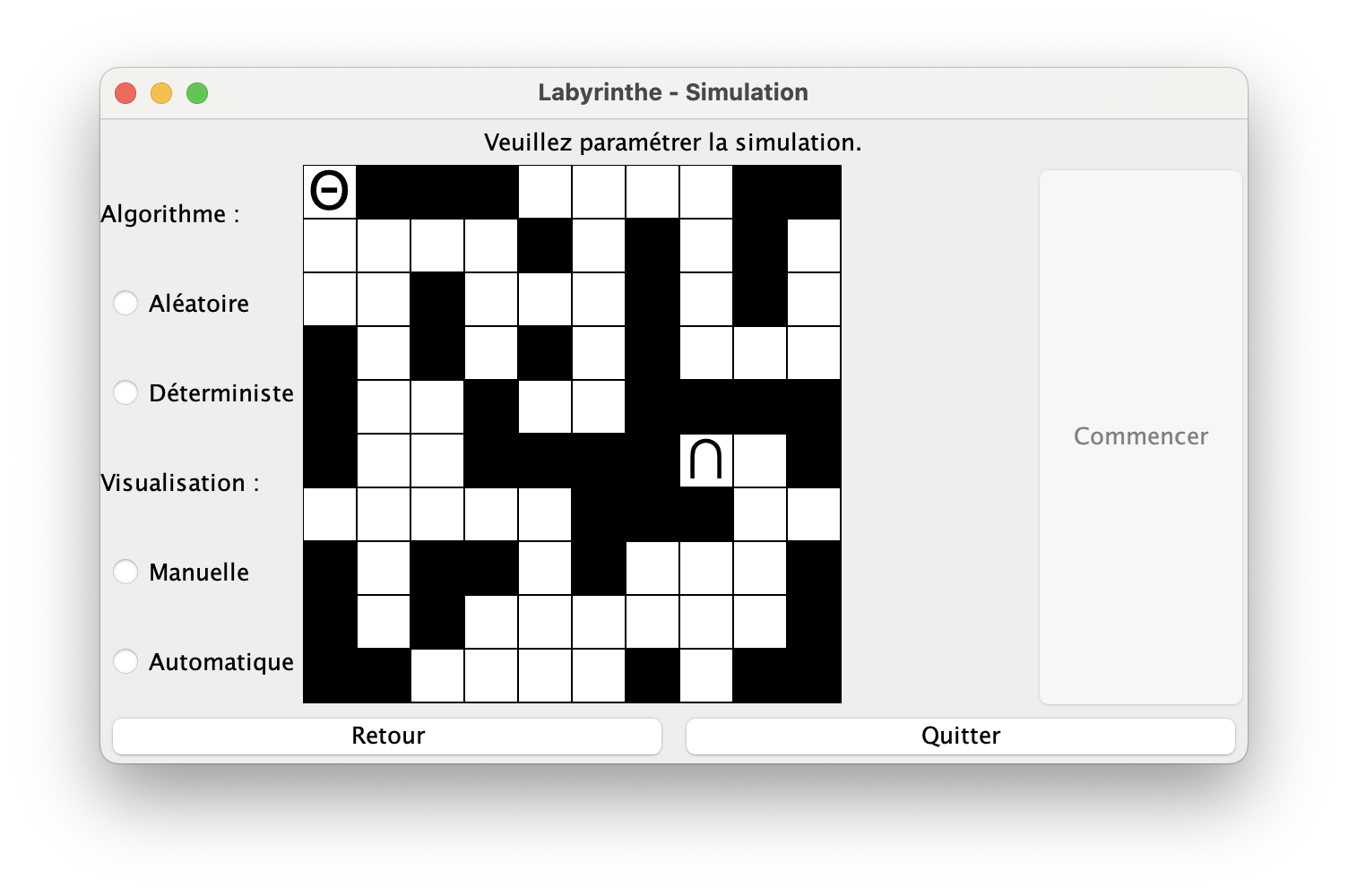Le premier algorithme est totalement aléatoire comme le prévoit la consigne, l'algorithme choisie une direction sur les quatre aléatoirement et essaye d'y déplacer Thésée. Si la case est libre, alors Thésée s'y rend, et ainsi de suite.
Lors de la visualisation automatique, on effectue ces essais de déplacement un certain nombre de fois avant d'en déduire que Thésée est bloqué.
L'algorithme déterministe tente, dans l'ordre, les directions Nord, Sud, Est puis Ouest. À la différence de l'algorithme aléatoire, il vérifie non seulement que la case n'est pas bloqué, mais aussi qu'il ne s'y ait pas déjà rendu auparavant via une pile. Tant qu'il y a des cases dans la pile, on continue :
- On regarde la case en haut de la pile (la case actuelle).
- Si la case actuelle est la sortie du labyrinthe, on a trouvé le chemin et on arrête l'algorithme.
- Sinon, on regarde les cases voisines non visitées de la case actuelle.
- Si on trouve une case voisine qui est valide (à l'intérieur du labyrinthe), non visitée et libre (pas de blocage), on l'ajoute à la pile et on la marque comme visitée.
- Si on ne trouve aucune case voisine non visitée, cela signifie que la case actuelle est un "cul-de-sac" et on la retire de la pile.
L'algorithme utilisé , qui est le parcours en profondeur (DFS), est garanti de trouver la sortie si un chemin vers la sortie existe. Voici une démonstration pour prouver cette propriété :
- Supposons qu'il existe un chemin de la case de départ à la sortie du labyrinthe.
- L'algorithme commence par la case de départ et explore systématiquement les voisins non visités jusqu'à ce qu'il atteigne la sortie ou qu'il n'y ait plus de voisins non visités à explorer.
- Comme l'algorithme utilise une approche déterministe, il explore chaque branche du labyrinthe jusqu'à son terme avant d'explorer une autre branche. Cela signifie qu'il visite chaque case possible dans le labyrinthe.
- Si la sortie est atteignable, l'algorithme finira par atteindre la case de sortie, car il examine tous les voisins non visités avant de revenir en arrière.
- Lorsque l'algorithme atteint la case de sortie, il s'arrête et indique que le chemin a été trouvé.
- Par conséquent, si un chemin existe dans le labyrinthe, l'algorithme de parcours en profondeur utilisé ici sera en mesure de le trouver.
La visualisation manuelle permet une visualisation de chaque étape de l'algorithme, comme ici avec l'algorithme aléatoire :
